sam781
Full Member level 4

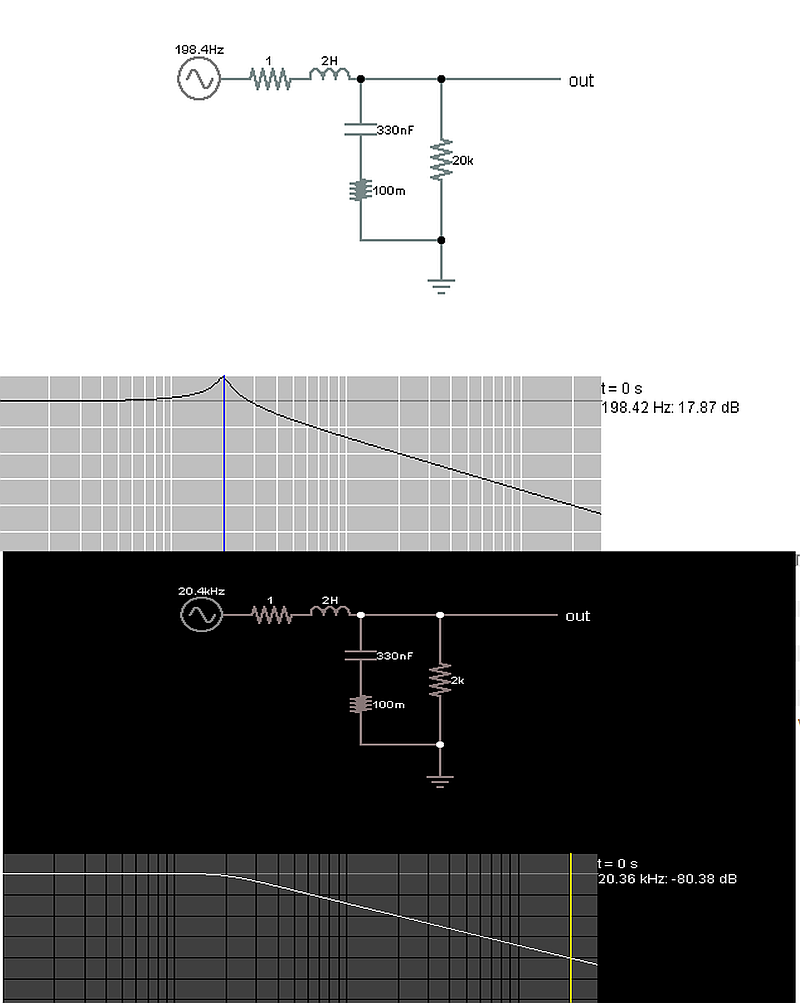
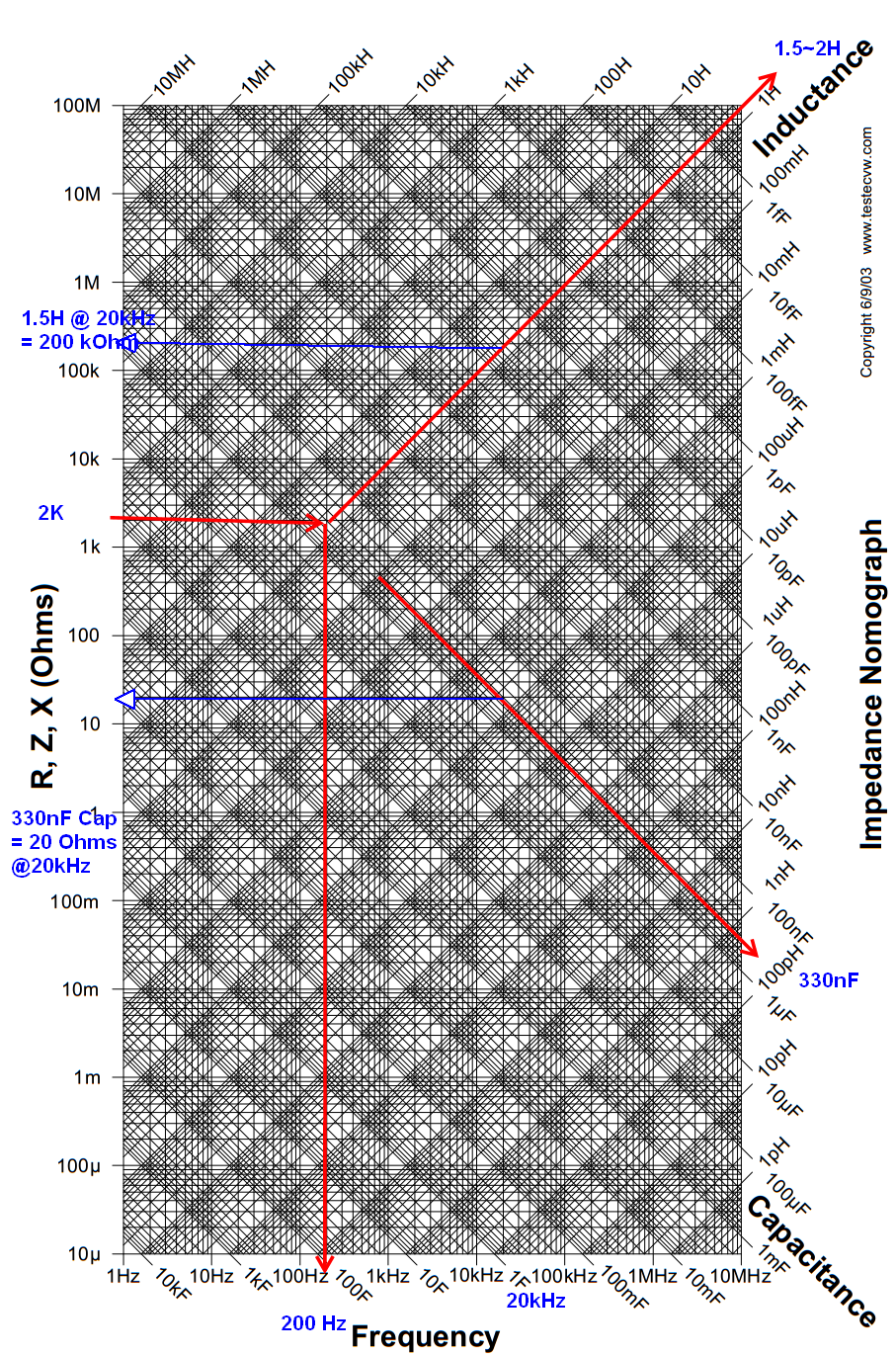
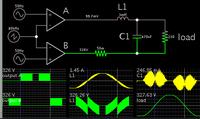
More detail info for the required converter -
Ripple voltage = 1%
Ripple current =10%
Full load = 1A (load for this converter will be an bridge inverter, final load can be inductive with pf 0.7)
Ripple voltage = 1%
Ripple current =10%
Full load = 1A (load for this converter will be an bridge inverter, final load can be inductive with pf 0.7)