Finding the input impedance of CCCS

[paulmdrdo]

Good day everyone! I need your help on this one. I'd like to derive the equation for the closed-loop input impedance of the circuit attached. The final form of the equation is also shown below.




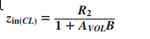
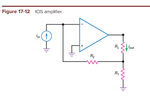
Here's what I have tried


I was stuck. Can you tell what other route I can take to go about this derivation? Thanks!

 

[FvM]

Zin(CL) formula is not correct, instead of R2, an effective resistance of R2 + RL||R1 must be put in.

 

[paulmdrdo]

Zin(CL) formula is not correct, instead of R2, an effective resistance of R2 + RL||R1 must be put in.

Is this the thevenin resistance seen by the source? I was able to make it appear in my derivation just a moment ago.

 

[FvM]

It's the impedance seen with Av = 0 and Rout = 0.

 

[sutapanaki]

One alternative derivation:

 

[paulmdrdo]

One alternative derivation:

View attachment 157333

Hi sutapanaki. Why do you assume that R1 is infinite?

 

[sutapanaki]

R1 is the resistor that complicates a bit the derivation of the input resistance. So, if it were not there, results will be easier. Assuming R1 infinite, I find those 3 things Rio, Rn and Rd. Then I combine them and re-introduce R1 back to get the final result.

 

[paulmdrdo]

R1 is the resistor that complicates a bit the derivation of the input resistance. So, if it were not there, results will be easier. Assuming R1 infinite, I find those 3 things Rio, Rn and Rd. Then I combine them and re-introduce R1 back to get the final result.

How did you get R2+RL/1+Av? I'd like to adapt your technique. The one I know is too involved. Yours seems fast. Can you refer me to a literature that explains this type of method?

 

[albbg]

You can easily find the input impedance using the superposition.

if Vo is the output of the op-amp, V+ its non-inverting input and V- its inverting input and Iin the stimulus:

1) exclude Iin, then (Va-) = Vo*RL/(R1+RL)
2) short Vo, then (Vb-) = Iin*[R1*RL/(R1+RL)+R2]

Applying superposition (V-)=(Va-) + (Vb-) = Vo*RL/(R1+RL)+Iin*[R1*RL/(R1+RL)+R2]

We know that Vo = A*[(V+) - (V-)], but (V+)=0 thus Vo=-A*(V-)

Substituting Vo:

V- = -A*(V-)*RL/(R1+RL) + Iin*[R1*RL/(R1+RL)+R2]

Zin = (V-)/Iin = [R1*RL/(R1+RL) + R2]/[1 + A*RL/(R1+RL)]

If we call, nw, B=RL/(R1+RL) we will have:

Zin = (R1*B+R2)/(1+A*B)

in case R2 >> R1*B then we can approximate Zin = R2/(1+A*B)

Sorry, in my derivation I exchanged the label R1 with RL (R1 is the output series and RL is to ground)

 

[paulmdrdo]

You can easily find the input impedance using the superposition.

if Vo is the output of the op-amp, V+ its non-inverting input and V- its inverting input and Iin the stimulus:

1) exclude Iin, then (Va-) = Vo*RL/(R1+RL)
2) short Vo, then (Vb-) = Iin*[R1*RL/(R1+RL)+R2]

Applying superposition (V-)=(Va-) + (Vb-) = Vo*RL/(R1+RL)+Iin*[R1*RL/(R1+RL)+R2]

We know that Vo = A*[(V+) - (V-)], but (V+)=0 thus Vo=-A*(V-)

Substituting Vo:

V- = -A*(V-)*RL/(R1+RL) + Iin*[R1*RL/(R1+RL)+R2]

Zin = (V-)/Iin = [R1*RL/(R1+RL) + R2]/[1 + A*RL/(R1+RL)]

If we call, nw, B=RL/(R1+RL) we will have:

Zin = (R1*B+R2)/(1+A*B)

in case R2 >> R1*B then we can approximate Zin = R2/(1+A*B)

Sorry, in my derivation I exchanged the label R1 with RL (R1 is the output series and RL is to ground)

Hi albbg. Thanks for your time. Can this method work when finding the output impedance?

I keep getting a wrong result. Here's what I did.



The negative feedback is supposed to increase the output impedance but my equation says otherwise. Can someone point out what did I do wrong in my derivations.

 

[Audioguru]

Negative feedback always decreases the output impedance. If something external tries to change the output voltage then the negative feedback sends the change to the inverting input to cancel the change.

 

[paulmdrdo]

Negative feedback always decreases the output impedance. If something external tries to change the output voltage then the negative feedback sends the change to the inverting input to cancel the change.

But it is aa Current controlled current source. Feedback's purpose here is to increase the output impedance.

 

[Audioguru]

Positive feedback (bootstrapping) increases the output impedance.

 

[paulmdrdo]

Positive feedback (bootstrapping) increases the output impedance.

Is my derivation correct though? My book says Zo = (1+AV)R1.

 

[sutapanaki]

How did you get R2+RL/1+Av? I'd like to adapt your technique. The one I know is too involved. Yours seems fast. Can you refer me to a literature that explains this type of method?

Look for Dr.Middlebrook's Extra element theorem. or any material regarding that.

 

[paulmdrdo]

Look for Dr.Middlebrook's Extra element theorem. or any material regarding that.

Hello sutapanaki, I just read about just now. In your solution, you used R1 to be the Extra element, can we choose other element of the circuit as the extra element and arrive at the same answer?

 

[sutapanaki]

Yes, you can choose another element as the extra element, of course. The formulation of the result will be different, because you will have to find Rn and Rd from the point of view of the new extra element. But you can always manipulate algebraically the results for different extra elements to look the same at the end. And of course, when you substitute the numerical values, you must get the same result.

 

[albbg]

Is my derivation correct though? My book says Zo = (1+AV)R1.

I presume you have to calculate the output impedance seen by the load, that is by RL. To do this you have to substitute the load with a generator and calculate the current flowing through the generator and the voltage across it, then apply Z=V/I.
I used a current generator and I did the following derivation (neglecting input and output impedance of opamp, I considered it as ideal, but the finite OL gain):



In this case we have a current generator so we need a very high impedance, ideally infinite. The feedback regardless to its value (the op-amp is ideal here) allows to greatly increase the impedance since the voltage is boosted by the OL gain of the amplifier.

 

[sutapanaki]

Applying Blackman's impedance formula gives the output impedance in 1 line. And yes, it is R1*(1+A)

 

[albbg]

Applying Blackman's impedance formula gives the output impedance in 1 line. And yes, it is R1*(1+A)

I think the application of the Blackman's theorem is not so immediate. The result, of course, is the same in any case some calculation have to be done.