Detection of sinusoids in the discrete sequence

[S-LifeLover]

Good day!
Please excuse me for my English.
I have the following problem:
There is a period of a discrete signal.
This signal is the sum of sinusoidal signals (sinusoids). These sinusoids not always begin and end at the beginning and end of the period.
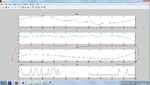
As an example, I suggest the following (see figure)
Period length = 300.
There are two sinusoidal signals: one signal all over the period (300), the second - only half of the period (150).
Question: how to detect both signals in this example? That is, how to determine the frequency of these two signals.
If both signals were all over the period, the usual Fourier (fft) would perform this task. But in this example, Fourier did not determine the frequency correctly.
Thank you in advance!

 

[Mityan]

Every signal is the sum of sinusoids.

The spectrum of periodic signal consists of discrete components.

The spectrum of single pulse has no discrete components (better to say has an infinite number of them - it's continuous).

To estimate a spectrum more precisely take more periods of your discrete signal together and apply fft.

 

[S-LifeLover]

Every signal is the sum of sinusoids.

The spectrum of periodic signal consists of discrete components.

The spectrum of single pulse has no discrete components (better to say has an infinite number of them - it's continuous).

To estimate a spectrum more precisely take more periods of your discrete signal together and apply fft.

Thanks for the reply!
This is so. But, unfortunately, I can not affect the original signal and can not increase the frequency of sampling.

 

[included]

You could move the second signal (the 150s/s) to the middle of a 300 sized block and pad the signal, apply say a hanning window and add it to the 300s/s signal also hanned and then FFT it - but you cant FFT a 150 or 300 block size so maybe use Winograd or multiple digital filters. Then you will find your frquency.

Alternately process the 150 samples and then invert the transform with 300s/s and then add them, or hann the 150s/s window and then copy it to the second half of the block, add it in etc etc.

Dont really see the problem here.

 

[FvM]

First comment, the second waveform in your initial post is wrong, because the signal is undefined for half of the period.

You may think of this point as a trivial drawing error. But it's also symptomatical for not considering the properties of the signals involved in the problem.

But in this example, Fourier did not determine the frequency correctly.

What do you exactly mean with this statement? Of course the signals show up in the FFT. I guess, the FFT didn't look like you exepcted it. But what's the problem? Do you know how an on/off keyed sine looks in a fourier transformation? Have you heard about windows and relation of sample length and frequency resolution?

In my view, you need to narrow down the problem:
- frequency range of involved signals
- required frequency resolution
- maximum number of signals
- minimal number of periods appearing in the measurement
- allowed modulation envelopes (only on/off or others)

You can also treat the problem as a model estimation: Assume a set of sine signals and modulation windows, estimate the parameters.

 

[S-LifeLover]

Thanks for the answers!
My example is really very simple.
I am in this example would draw your attention to the following: If the sine wave is not defined on the whole window and when it intersects with other unknown sinusoid, the Fourier is not exactly determine the frequency.
Of course, we can take a smaller window, but ....
How about this example:
Note that I am defining period of sinusoid (not the frequency). That is, how many points should be sinusoid to make the full period. Sorry, but I feel so comfortable.
In my example, sinusoids with three different lengths, with different periods (frequencies). It are put together and create a new signal.
Objective: to determine the period (frequency) of the source sinusoids.

function [ ] = Test()
    x = 1:100;
    y1 = CreateSin(x, 20, 78, 30);
    y2 = CreateSin(x, 13, 60, 45);
    y3 = CreateSin(x, 3, 100, 60);
    y = y1 + y2 + y3;
    subplot(4, 1, 1);
    plot(x, y1);
    axis([0, 100, -2, 2]);
    subplot(4, 1, 2);
    plot(x, y2);
    axis([0, 100, -2, 2]);
    subplot(4, 1, 3);
    plot(x, y3);
    axis([0, 100, -2, 2]);
    subplot(4, 1, 4);
    plot(x, y);
    axis([0, 100, -2, 2]);
end

% function create sinusoid
% x - domain
% begin - point from which to begin a sinusoid
% finish - the point at which ends sinusoid
% period - sinusoid period
function [ y ] = CreateSin(x, begin, finish, period )
  y = zeros(1, length(x));
  y(begin:finish) = y(begin:finish) + sin(x(begin:finish) * 2 * pi / period);
end

This example is not so simple. Because there is sinusoids is almost completely overlap. And sinusoids very short. This makes the task very difficult.
I would be grateful for any ideas

 

[included]

It seems you are trying to push fourier analysis beyond its limits.

First - have you run a digital filter over your block before converting to frquency?
Second - have you chosen a realistic sample period, you need to check the frequency resolution of the final result and do your sinusoids sit exactly on a bin or slighly off the bin. Are the sinusoids even in a bin?

Please define your whole process in words as well as code to see exactly what you are doing.

 

[FvM]

I am in this example would draw your attention to the following: If the sine wave is not defined on the whole window and when it intersects with other unknown sinusoid, the Fourier is not exactly determine the frequency.

I think the statement misses the point. The fundamental of the sine segments will still show as peaks in the fourier transformation. Unfortunately you don't show the spectrum.

But the abrupt cuts are adding broad bands to the spectrum. It's not exactly caused by the zeroed part of the sine, the same thing happens if you transform a sine that completely fills the window, but it's period isn't an integer part of the sequence length.

It seems you are trying to push fourier analysis beyond its limits.

Yes. Fourier analysis shows you the spectrum of a signal as you defined it. Apparently you want a spectral analysis, that shows an arbitrary part of the spectrum and ignores the rest.

 

[included]

But the abrupt cuts are adding broad bands to the spectrum. It's not exactly caused by the zeroed part of the sine, the same thing happens if you transform a sine that completely fills the window, but it's period isn't an integer part of the sequence length.

The sharp cut off will look like an impulse and have broad band noise added as you say. I also think if I read his code correct he has a 60 Hz sine wave in a sample window of 100? Aliasing seems probable here unless I mis read the code. But I do not use Matlab so cant really comment till the OP puts some flesh on the problem.

 

[FreeMAn0110]

Another issue with this waveform is that the waveform is incomplete. He has not defined the waveforms for the complete sample space. Hence non of those can be considered to be sinusoidals. It is important to define the sinusoidal for the complete sample space. Or else use windowing I guess.

 

[FvM]

I also think if I read his code correct he has a 60 Hz sine wave in a sample window of 100?

No, it's a period of 60 for signal length of 97, about 1.5 periods. It's not an alias problem.

Another issue with this waveform is that the waveform is incomplete. He has not defined the waveforms for the complete sample space.

Other than in the initial post, the waveform is completely defined, being zero outside the defined sine period. That's by design of the problem, but of course, the spectrum will reflect the signal as it's defined.

 

[FreeMAn0110]

Other than in the initial post, the waveform is completely defined, being zero outside the defined sine period. That's by design of the problem, but of course, the spectrum will reflect the signal as it's defined.

Since the sample set has zeroes in the sample space for the sine way, it no longer stays as a sine way. May I am understanding you in a wrong way, but the when the sample for a particular signal becomes zero, we wont be able to call it a sine way right. Please correct me if I have understood things wrongly.

- - - Updated - - -

I think I have understood what you are trying to explain. By design the signal are supposed to be zero outside the interval. Sorry for the trouble. I was thinking you were trying to create a sum of sine waves and then consider the sample space 0-100.

 

[FvM]

but the when the sample for a particular signal becomes zero, we wont be able to call it a sine way right.

Yes, or we can say it's an on-off-keyed sine, which causes the observed wide band signals in the spectrum.

 

[S-LifeLover]

Excuse me for long silence. My dog ate my English-Russian dictionary. I had a long time to translate without a dictionary.
Just kidding.

First - have you run a digital filter over your block before converting to frquency?

No, I do not use filters. In this example, the signal clean. That is, there is no interference. Therefore I think that the filters are not needed. I may be wrong. If you think that the filter should be used, advise what, please.

Second - have you chosen a realistic sample period, you need to check the frequency resolution of the final result and do your sinusoids sit exactly on a bin or slighly off the bin. Are the sinusoids even in a bin?

I do not speak English, so I may have misunderstood.
Sinusoids do not sit exactly on bins in the spectrum. Moreover, the problem statement, I do not know anything about the sinusoids that make up the source signal. It does not ensure that the sinusoids sit exactly on bins.

Please define your whole process in words as well as code to see exactly what you are doing.

My problem is the following:
There is source signal (sequence data).
Need to find a sinusoids (or other periodic functions) in the signal. To find patterns in the behavior of the signal.
I could show you a lot of the algorithm, in which I tried to use the Fourier transform, but neither solves the problem. I will try soon to write here one algorithm. Can you help find fresh solutions for me

But the abrupt cuts are adding broad bands to the spectrum. It's not exactly caused by the zeroed part of the sine, the same thing happens if you transform a sine that completely fills the window, but it's period isn't an integer part of the sequence length.

This is what I wanted to say. I know absolutely nothing about the sinusoids that make up the signal. So I do not know how to decipher the Fourier spectrum. If I was sure that all the signals were all over the window, then any leakage I could interpreted as sinusoid is out of bean.
This makes me think that the Fourier can not be answered, for example, the question: where the beginning and end of the sinusoid with a period = 30.

Yes. Fourier analysis shows you the spectrum of a signal as you defined it. Apparently you want a spectral analysis, that shows an arbitrary part of the spectrum and ignores the rest.

I'm afraid I misunderstood you.
My goal is not meant to receive spectrum. My objective implies that it is necessary to find the properties of each sinusoid that make up of a signal (amplitude, frequency (period), the phase of the beginning and end). Perhaps, for this task I have to use a lot of different spectra obtained at different windows. Or even not use the Fourier spectra. The main thing - to find a property sinusoid to reproduce the source signal as the sum of sinusoids, not as a sequence of points.

The sharp cut off will look like an impulse and have broad band noise added as you say. I also think if I read his code correct he has a 60 Hz sine wave in a sample window of 100? Aliasing seems probable here unless I mis read the code. But I do not use Matlab so cant really comment till the OP puts some flesh on the problem.

Can be more about momentum? What instrument can be found or measure this momentum?
In my code, 60 and 100 - it is not the frequency. This period.
Signal in my example - the data sequence. For example, the temperature at a certain hour. We can say that the temperature goes up and down periodically with a period of 24 hours. And what if the frequency of a temperature? 1/24? And in which case units to measure this frequency? fluctuation in an hour? It is not convenient. That's why I define a sinusoid in the period. For example, to look at the sinusoid and say here it is repeated every 30 hours.

Another issue with this waveform is that the waveform is incomplete. He has not defined the waveforms for the complete sample space. Hence non of those can be considered to be sinusoidals. It is important to define the sinusoidal for the complete sample space. Or else use windowing I guess.

That's right! But, unfortunately, the conditions of the problem, as parents, do not choose.
I can use windowing. But, unfortunately, I was not successful in this regard.
Maybe later I will give an algorithm that was used.

No, it's a period of 60 for signal length of 97, about 1.5 periods. It's not an alias problem.
Other than in the initial post, the waveform is completely defined, being zero outside the defined sine period. That's by design of the problem, but of course, the spectrum will reflect the signal as it's defined.

All right. Thank you for understanding my problem.

Since the sample set has zeroes in the sample space for the sine way, it no longer stays as a sine way. May I am understanding you in a wrong way, but the when the sample for a particular signal becomes zero, we wont be able to call it a sine way right. Please correct me if I have understood things wrongly.

Here is a fantastic example:

Imagine a planet. The water level at the beach depends on the moon. We all know that the moon pulls the water. And on the last day of our planet 100 Earth hours.
Here's the plot:


Now imagine that we have a second moon, which rotates twice as fast around the planet (the period is 50 Earth hours)
Moons can be at one point, or can on the different sides of the moon. Therefore, the gravitational force of the two moons are summarized as two vectors, so we get the following picture.


And that's not all. Second Moon permanently disappear somewhere. No one knows where. Just disappears. So when the second moon is absent the effect of gravity on the water only to the first moon.
Our second moon appears stable at 27 o'clock, and disappears by 64 o'clock


Add to our skies third moon:


Now imagine that we want to know about when the moon disappear. We also need to know how fast to spin the moon around the planet. And all this we can know, having the only the graph (the water level):

Who has ideas how to do this algorithmically?

function [ ] = Run()
    close all;
    clear all;
    clc;

    moon1 = CreateMoon(100, 1, 100, 100);
    moon2 = CreateMoon(100, 27, 64, 50);
    moon3 = CreateMoon(100, 50, 70, 75);
    
    subplot(4, 1, 1);
    plot(moon1, '.');
    axis([0, 100, -2, 2]);
    subplot(4, 1, 2);
    plot(moon2, '.');
    axis([0, 100, -2, 2]);
    subplot(4, 1, 3);
    plot(moon3, '.');
    axis([0, 100, -2, 2]);
    subplot(4, 1, 4);
    plot(moon1+moon2+moon3, '.');
    axis([0, 100, -2, 2]);
end

% function create moon
% dayLength - the number of hours in a day
% appearance - time of appearance
% disappearance - time of disappearance
% period - time for a complete orbit around the planet
function [ y ] = CreateMoon(dayLength, appearance, disappearance, period )
  x = 1:dayLength
  y = zeros(1, length(x));
  y(appearance:disappearance) = y(appearance:disappearance) + sin(x(appearance:disappearance) * 2 * pi / period);
end

 

[FvM]

You have created artificial signals with discontinuities that are far from any real world signals. Choosing signals like this also suggests that you don't have much understanding about the relation of time to frequency domain. These signals will have disastrous effects in the fourier domain.

In my view, you have tightend your requirements by saying you want to determine start and end time and phase of each signal component (Or at least have told it clearly now).

I think, that the approach I sketched in post #5 ("model estimation") is the most promising method to solve the problem. The main point is that you can restrict the set of possible signals, e.g. to on-off keyed sine waves in a particular frequency and magnitude range. The fourier domain presentation can be still helpful to identify the strongest spectral "lines" as a starting point for the model.

 

[S-LifeLover]

You have created artificial signals with discontinuities that are far from any real world signals. Choosing signals like this also suggests that you don't have much understanding about the relation of time to frequency domain. These signals will have disastrous effects in the fourier domain.

You are right. But the solution to this problem will bring me one step more to the difficult and real problem. For example, it will be possible to study the signals that do not appear suddenly, but gradually. That is, they are slowly increasing in amplitude (born) and slowly decrease in amplitude (decay). For example, it could be coming from far away meteorite, which will also affect the water level in our imaginary planet

In my view, you have tightend your requirements by saying you want to determine start and end time and phase of each signal component (Or at least have told it clearly now).

Yes.

Do you know how an on/off keyed sine looks in a fourier transformation

Maybe I do not understand how we can "on/off keyed sine looks in a fourier transformation". Could you explain it.
If I understand you correctly, you offer subtracted from the original signal sinusoid, which is built using the Fourier coefficients. But we can not build a sinusoid of the Fourier coefficient, because we have a huge "leak".
My task is to find a way decomposition signal.

Have you heard about windows and relation of sample length and frequency resolution

Of course, the first coefficient is equal to a constant, the second corresponds to a sinusoid with a frequency of 1. The third coefficient corresponds to a sinusoid with a frequency of 2, etc.

In my view, you need to narrow down the problem:
- frequency range of involved signals
- required frequency resolution
- maximum number of signals
- minimal number of periods appearing in the measurement

Sadly, I can not place restrictions on the signal. If your convenience, we can create a signal according to your criteria. But as a temporary solution, which will help us to find a solution for a given example of the planet and moons.

- allowed modulation envelopes (only on/off or others)

Can you tell me more about this, please.

You can also treat the problem as a model estimation: Assume a set of sine signals and modulation windows, estimate the parameters.

Can you explain this approach by the example of our moon?
I see the signal as a set of sinusoidal signals. The question is how to find this set

he main point is that you can restrict the set of possible signals, e.g. to on-off keyed sine waves in a particular frequency and magnitude range. The fourier domain presentation can be still helpful to identify the strongest spectral "lines" as a starting point for the model.

Can you demonstrate how you can do this in our example with moons, operating only the sum of signals. That is, in your possession is not a set of source signals, but only their sum.






I am interested in a method that, in my view, better helps to solve my problem: Empirical Mode Decomposition (EMD)
Look what results achieved by the example with moons

Unfortunately, we were able to identify only one moon (which is the full width of the window). But we were able to algorithmically find at least one of the signal composes. I think this is a good start to finding a solution.

moon1 = CreateMoon(1000, 1, 1000, 100);
moon2 = CreateMoon(1000, 340, 1000, 33);
moon3 = CreateMoon(1000, 1, 700, 70);

Look at the results and compare them to the sine wave. Of course, there is no 100% accurate. But we're just getting started.
I marked in red pencil, which would have placed the boundary of the sine wave and their periods.

Can you tell us anything about the EMD, that would help me move on?

 

[included]

I am begining to understand your question as you explain it further. Once you have added the various time signals together to a single signal the information about their original composition is lost and you cannot get it back. All you can do is analyse the new composite signal you have.

You may like to try a recursive coherance technique to show when the signal starts and stops (within the resolution of your correlation window) but you cant recreate lost data by any technique.

There are a number of ways to 'seek' your frequency and where it is maximal in the frame but the processing is quite complex or more I should say processor intensive. You could detect the main frequencies in the composite signal and then apply for each frequency a correlation across the whole signal with a variable length sine wave at the frequency of interest. It is not a new technique but may solve your problem.

 

[S-LifeLover]

I am begining to understand your question as you explain it further. Once you have added the various time signals together to a single signal the information about their original composition is lost and you cannot get it back. All you can do is analyse the new composite signal you have.

Yes.

There are a number of ways to 'seek' your frequency and where it is maximal in the frame but the processing is quite complex or more I should say processor intensive. You could detect the main frequencies in the composite signal and then apply for each frequency a correlation across the whole signal with a variable length sine wave at the frequency of interest. It is not a new technique but may solve your problem.

Thank you very much for the help! Could you specify the source where I could read about this technique?

 

[included]

I do not know of any sources where the method is described and much of the the technique we coded and used years ago to solve specific problems.

I do not code in Matlab so cant help out with examples but I can explain the method for you to code. It is better that way as you will understand the process and be able to interpret the results better.

So lets start with a block of data say 100 samples long that has several chirps within it starting and stopping at unknown points. Call it block 1 or B1

Now define a new block length of say n. Call it B2 and create inside it a sine wave.

Now overlay B2 on to of B1 so the B2 starts at the first point in B1 and multiply the blocks and sum the result. Store it. Just sum the result of B1*B2 and exclude the rest of B1.

Now move B2 1 point at a time across B1 and repeat the process until the B2 reaches the end of B1. Process P1.

Now change the phase in B2 sine wave by shifting it 1 point through out the block and repeat the process P!. Shift the point again and so on till you have covered all the possible phase angles. Process P2.

When you study the results there will be one or two of these overlays that gives a maxima.

Now change the size of B2 by 1 sample and repeat the whole process of P1 and P2

Next change the sine frequency and repeat all the above steps. So P1 and P2 and P3.

Eventually you will find an absolute maxima in the results and that is the closest you can get to solving for that chirp.

If you understand the procedure you can write some simple DO LOOPS with nested LOOPS and increment the block size, change the phase and restart the process with the next frequency, it is quite simple.

So if you understand this and do code it up remember that the next procedure uses block B3 which is offset from B2 and B2 is then cross spc'ed with B3 as it moves and the coherance then obtained. The coherance is then used as a confidence indicator to show if you have chosen the correct block size n, freq of sine , position and length and phase.

I used it to great effect with a decaying signal to show the point where internal dissipation took over from the input energy, also lends itself well to display by a waterfall diagram as all the data can be visualised in one display.

Hope you have an i7 to do this lot!!!

 

[S-LifeLover]

Thank you very much for the detailed explanation
A few questions:
1) Can you explain what "chirps"
2) I'm sorry, I did not understand the phrase "... and exclude the rest of B1.". What is the "rest of B1"?

I've experimented with a procedure like this. But, alas, my i3 not enough process more or less serious example. To provide the desired accuracy, for my task calculation process extends for several years, alas.