- Joined
- Jan 22, 2008
- Messages
- 53,660
- Helped
- 14,809
- Reputation
- 29,911
- Reaction score
- 14,422
- Trophy points
- 1,393
- Location
- Bochum, Germany
- Activity points
- 303,427
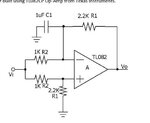
I prefer the usual view that treats the OP as black box with specified transfer characteristic and restricts the analysis to feedback in the external circuit.I think, following this philosophy, even the simplest opamp amplifier (inverting, non-inverting) would be classified as multiple feedback circuits.
I doubt, if this is a definition that makes sense. What about feedback caused by the collector-base capacitance of a BJT?
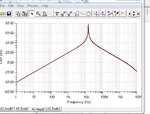
Referring to the previous discussion it should be underlined, that a complex pole pair can be generated without multiple feedback pathes, as you can see from a second order Sallen Key filter with ideal amplifier.