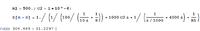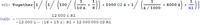[SOLVED] Calculate values in a transformer

[The Electrician]

Feels like I'm doing so much errors as it is possible to do here, thanks for sticking with me through this!

So the impedance at Zb is: 1/Zb=1/(3000j)+1/(800 -0.00016j) <=> Zb=746.888 + 199.17j

Assuming I did the calculation in Z(A-B) correctly, ill just replace the figures; Impedance at Z(A-B): 1/Z(A-B)=(0.002j)+1/(746.888+199.17j) <=> Z(A-B)=288 -384j

I get:

Z(A-B): 1/Z(A-B)=(0.002j)+1/(746.888+199.17j) <=> Z(A-B)=304.489 + 31.23j

If I carry 12 digits through all the intermediate calculations, I get:

Z(A-B) = 304.4892648 + 31.22966818j

- - - Updated - - -

In the image attached to post #1, the current source is labeled:

IO(t)
1A

But in some text below that it says: IO(t) = 10sin(1000t) (mA)

Which is it? Is the source a 1 amp source, or a 10 mA source?

 

[Hatmpatn]

Looking at the original schematics, I really have no idea why I wrote that it is a 1A current source. The correct value is 10mA...

 

[The Electrician]

By the way, in the image of post #18 you have the two capacitors C1 and C2 labeled with an impedance of 1000j, but they should be -1000j.

Have you recalculated Z(A-B) to see if you get the same thing I get? I make mistakes, too, so you should check my results.

Now you have the impedance of the circuit at terminals A-B as (304.489 +31.23j). That is also in parallel with the internal impedance of the source which is (70.7107 + 70.7107j). Calculating the parallel equivalent of these two we get (63.9671 + 45.8904j).

We can use ohm's law for AC circuits to calculate the voltage across the A-B terminals. Ohm's law says that V = I*R. For AC circuits it becomes V = I*Z. We have Z = (63.9671 + 45.8904j), so V = .01*(63.9671 + 45.8904j) = (.639671 + .458904j) volts. This is also the voltage at the N1 terminals of the transformer; the voltage at the N2 terminals is 1/10 of that but it's in phasor form. Now you have to find an expression for U(t) in terms of a sine function with a phase shift.

 

[Hatmpatn]

Yes, it should still be correct since you corrected my calculation there with -1000j+4000j=3000j.

Given that the we have the voltage V = (0.639671 + 0.458904j) V

Converting this should give us;
|V|= √(R²+α²), where α is our complex part. <=> √(0.40917899+0.2105929)=0.787256
(V)= arctan(α/R) = 1.095480

Our V = 0.787256*e^j1.095480

Which is u(t)=0.787256sin(1000t+1.095480) [V]

Maybe? :thumbsup:

 

[The Electrician]

Yes, it should still be correct since you corrected my calculation there with -1000j+4000j=3000j.

Given that the we have the voltage V = (0.639671 + 0.458904j) V

Converting this should give us;
|V|= √(R²+α²), where α is our complex part. <=> √(0.40917899+0.2105929)=0.787256
(V)= arctan(α/R) = 1.095480

Our V = 0.787256*e^j1.095480

Which is u(t)=0.787256sin(1000t+1.095480) [V]

Maybe? :thumbsup:

You've calculated the angle as arctan(R²/α²) = 1.095480[/B]

It should be arctan(α/R) = .6223128[/B]

Now you need to calculate the real power and the reactive power in the load.

From your first post you have:

b) Calculate the "active effect"(P=U*I*cosφ=RI²) and the "reactive effect" (Q=U*I*sinφ=XI²) that is obtained in the load R2-L2.

U is the magnitude of the voltage across the parallel combination of R2 and L2.

I is the magnitude of the total current through the parallel combination. You get the complex current by dividing the complex voltage at N2 by the equivalent impedance of R2 in parallel with L2, then calculating the magnitude of that current.

The angle φ is not the angle of the voltage, but is the angle of the equivalent impedance of the parallel combination of R2 and L2.

What do you get for P and Q?

 

[Hatmpatn]

Yes, ofcourse. I'm super sloppy...

u(t)=0.787256sin(1000t+0.6223128) [V]

Ill use this formula this time, since I failed every other time; Zp = (Z1*Z2)/(Z1 + Z2)

Z(R2)=8Ω
Z(L2)=10j

Gives our Z=(8*10j)/(8+10j)=4.87804878+3.902439024j

Hmm, guess we know this from before, haha.

S=Ue/Z=(U(hat)/√2)*1/Z, Where U(hat)=0.787256

=> 0.556674/(4.87804878+3.902439024j) = 0.0695843 - 0.0556674j

So P= 69.58mW
Q= 55.67mVA

I did it a little bit different than you told me, since I was reading this in my book. If this isn't correct, just tell me and I'll do it your way. Thank you!

 

[The Electrician]

Looking at your post, I just realized something.
The expression for the current source is: IO(t) = 10sin(1000t) (mA)

The value 10 is the peak current, not the RMS current. We need to do the calculations in terms of the RMS current which is 10/SQRT(2) mA. This changes the value of the complex voltage across A-B; it becomes (45.2316+32.4494j) volts.

I can't respond more fully because I have some things to do this afternoon, but i'll get back to this later.

You might want to reconsider all your calculations taking this into account.

 

[The Electrician]

Yes, ofcourse. I'm super sloppy...

u(t)=0.787256sin(1000t+0.6223128) [V]

Ill use this formula this time, since I failed every other time; Zp = (Z1*Z2)/(Z1 + Z2)

Z(R2)=8Ω
Z(L2)=10j

Gives our Z=(8*10j)/(8+10j)=4.87804878+3.902439024j

Hmm, guess we know this from before, haha.

S=Ue/Z=(U(hat)/√2)*1/Z, Where U(hat)=0.787256

=> 0.556674/(4.87804878+3.902439024j) = 0.0695843 - 0.0556674j

So P= 69.58mW
Q= 55.67mVA

I did it a little bit different than you told me, since I was reading this in my book. If this isn't correct, just tell me and I'll do it your way. Thank you!

OK, first of all, this:

u(t)=0.787256sin(1000t+0.6223128) [V]

is not u(t); it's u(A-B). U(T) is 1/10 of u(A-B) because of the 1:10 step down ratio of the transformer. It should be:

u(t)=0.0787256sin(1000t+0.6223128) [V]

Next, you need to square the voltage as shown in red:

S=Ue/Z=(U(hat)/√2)^2*1/Z, Where U(hat)=0.787256

=> 0.556674^2/(4.87804878+3.902439024j) = 0.000387358 - 0.000309886j

------------------------------------
For the last part of your problem you will need to recalculate Z(A-B), but with R1 and C2 left as symbolic variables. Then you will need to find values for R1 and C2 such that Z(A-B) is the complex conjugate of the internal impedance of the current source.

You might want to look at:

https://en.wikipedia.org/wiki/Maximum_power_transfer_theorem

Look under the sub heading "In reactive circuits".

 

[Hatmpatn]

Since we get our S = 0.000387358 - 0.000309886j , we should get, assuming that I did last time correctly, this;

P= 0.387358mW
Q= 0.309886mVA

I'm reading up on Maximum Transfer Theorem right now, ill get back in a little while.

----------------------------------------

I think we've made an error: This is the calculation we made for Z:

1/Z(A-B)=(0.002j)+1/(746.888+199.17j) <=> Z(A-B)=304.489 + 31.23j

Shouldn't there just be a 0.002, without the j? Since the resistance R1, is just an ordinary resistance? 1/500 as the impedance. Or am I forgetting something that we've already been through?

I stumbled on this when I tried to replace the 0.002j with just R1, which I am supposed to do right? And also replace C2 in the earlier calculations..

 

[The Electrician]

Since we get our S = 0.000387358 - 0.000309886j , we should get, assuming that I did last time correctly, this;

P= 0.387358mW
Q= 0.309886mVAR

I'm reading up on Maximum Transfer Theorem right now, ill get back in a little while.

The units of Q are VARs. See:

I think we've made an error: This is the calculation we made for Z:

Shouldn't there just be a 0.002, without the j? Since the resistance R1, is just an ordinary resistance? 1/500 as the impedance. Or am I forgetting something that we've already been through?

I stumbled on this when I tried to replace the 0.002j with just R1, which I am supposed to do right? And also replace C2 in the earlier calculations..

You're quite correct; the j doesn't belong. In post #21 I failed to notice the j, and my calculation was carried out without it.

If I do the calculation with the .002j, I get the same result you did, 288 -384j, which is incorrect.

 

[Hatmpatn]

Alright, then the final answer is:

P= 0.387358mW
Q= 0.309886mVAR

We had that
1/Za=(+.001j)+1/(487.805+390.244j) <=> Za=800 -0.00016j
1/Zb=1/(3000j)+1/(800 -0.00016j) <=> Zb=746.888 + 199.17j
1/Z(A-B)=(0.002j)+1/(746.888+199.17j) <=> Z(A-B)=304.489 + 31.23j

Replacing the values for R1 and C2 with just the names of them gives us:

1/Za=1/C2+1/(487.805+390.244j) <=> Za=C2(487.805+390.244j)/(487.805+390.244j+C2)
1/Zb=1/(3000j)+1/(C2(487.805+390.244j)/(487.805+390.244j+C2)) <=> superhairy problemsolving, which I cannot solve by hand..
So I guess im not doing it correcly am I?

 

[The Electrician]

Alright, then the final answer is:

P= 0.387358mW
Q= 0.309886mVAR

We had that
1/Za=(+.001j)+1/(487.805+390.244j) <=> Za=800 -0.00016j
1/Zb=1/(3000j)+1/(800 -0.00016j) <=> Zb=746.888 + 199.17j
1/Z(A-B)=(0.002j)+1/(746.888+199.17j) <=> Z(A-B)=304.489 + 31.23j

Don't propagate the error of having a J in there.

Replacing the values for R1 and C2 with just the names of them gives us:

1/Za=1/C2+1/(487.805+390.244j) <=> Za=C2(487.805+390.244j)/(487.805+390.244j+C2)
1/Zb=1/(3000j)+1/(C2(487.805+390.244j)/(487.805+390.244j+C2)) <=> superhairy problemsolving, which I cannot solve by hand..
So I guess im not doing it correcly am I?

You don't use the impedance of C2 in this expression:

1/Za=1/C2+1/(487.805+390.244j)

You use the admittance. Also, you need a jω in there:

1/Za=j ω C2+1/(487.805+390.244j)

Or, 1/Za=1000 C2 j +1/(487.805+390.244j)

It does get complicated. I'm very surprised they give a problem like this in a basic course, which is what you said you are taking.

Do you have any mathematical software available such as Matlab, Mathcad, Mathematica, etc., to help you with the calculations? Or, do you only have access to web resources such as Wolfram Alpha?

You're going to end up with a complicated expression which can be put in the form of a fraction. You will need to rationlize that fraction, so read this:

**broken link removed**

 

[Hatmpatn]

Well, It's a college course so I guess the level of difficulty is slightly higher than normally, but it is an introductory course to electronics.

I do have matlab, but i'm not familiarized with solving these kinds of equations with that program.

Do you use matlab? Would you please take a screenshot on how to solve these kind of equations in matlab?

 

[The Electrician]

I don't have Matlab; I have Mathematica.

When I first started on this problem I used my HP50 calculator, which can do complex arithmetic. But I can't conveniently post images from the HP50, so I did the calculations over again with Mathematica. Here's how it looks:



You should be able to do that with Matlab.

If you have an expression like that in Matlab, but with R1 and C2 kept as symbolic variables, you should be able to get an expression for Z(A-B).

Then you have to vary R1 and C2 until Z(A-B) becomes 70.71-70.71j

Matlab probably has a "Solve" function of some kind. You will have to separate the real and imaginary parts of your expression, set the real part to 70.71 and set the imaginary part to -70.71. This will give you two equations to be solved simultaneously.

 

[Hatmpatn]

Turns out my school offers mathematica. I'm still working on how to set up the equations, so this might take a little while.

I guess replacing R1 and C2 values with symbolic variables leaves us this equation:



So if I understand you correctly, this equation needs to be separated into a real part and an imaginary part.

The R1 should be varied so that the real part is = 70.71
And C2 should be varied so that the imaginary part is = -70.71

?

 

[The Electrician]

Turns out my school offers mathematica. I'm still working on how to set up the equations, so this might take a little while.

I guess replacing R1 and C2 values with symbolic variables leaves us this equation:

View attachment 110153

You have two errors. Where you have 1000C2i you need to have 1000 C2 i; leave a space between 1000 and C2, and between C2 and i. Without those spaces, Mathematica will consider 1000C2i a single variable. Leaving the space is taken to be multiplication by concatenation. To be extra sure, you can use * to mean multiplication, like this: 1000*C2*i

The other error is that you have R1 where you should have 1/R1; remember you're adding up admittances.

Now, to add to your workload, you will have to learn to use Mathematica (at least a little bit)!

So if I understand you correctly, this equation needs to be separated into a real part and an imaginary part.

The R1 should be varied so that the real part is = 70.71
And C2 should be varied so that the imaginary part is = -70.71

?

This is correct. You could assign numerical values to R1 and C2 and evaluate the expression you have, closing in on the correct values by trial and error. You might try that just for practice with Mathematica. Set R1=500 and C2=10^-6 and see if you get the value we got earlier in the thread for Z(A-B).
Here's the result you get when you do this:



Then try assigning other values to R1 and C2 to see if you can get close to Z[A-B] = 70.71 - 70.71j

The proper way to solve for R1 and C2 is to convert the expression for Z[A-B] into a fraction, then rationalize the fraction--convert the denominator into a pure real by multiplying the numerator and denominator by the conjugate of the denominator.

See the link I gave you in post #32.

Then you can separate the numerator into real and imaginary parts. You then put the real part over the denominator, giving you one fraction, Rpart/D. Put the imaginary part over the denominator giving you another fraction, Ipart/D. Now set these fractions equal to the real and imaginary parts of the desired impedance; this will give you two equations which must be solved simultaneously for R1 and C2.

Here's how Mathematica can convert the expression into a fraction:



Now see if you can rationalize this fraction.

 

[The Electrician]

I should say something about your comments:

"The R1 should be varied so that the real part is = 70.71
And C2 should be varied so that the imaginary part is = -70.71"

Varying R1 will change both the real and imaginary part of Z[A-B], not just the real part.
Similarly, varying C2 will also change both parts of Z[A-B]. This is why both equations must be solved simultaneously.

 

[tony_lth]

Hi, when calculated R1, I got ZAB=304.49+21.23j

 

[Hatmpatn]

After hours of searching for a way to solve this complex 2-variable equation, I must admit myself beaten.

I have tried to solved this equation using Matlabs function "Solve" but without success.
Now, I have this, and cant get anywhere..

I have also tried testing myself with random values on R1 and C2, without gotten close to the wanted values.

 

[Hatmpatn]

Well, after some further thinking, I tried to get rid of the fraction by multiplying the denominator of the left side with the right side of the equation. I then divided them up and got the a real part and a complex part, which led to two equations with two unknowns(solvable).



This gave me a C=7.7834952760308995818357410086380922120252412599 × 10^-6 and an R=155.22866075223847852020458253918194408260088579303157

But putting this into the equation gives me 76.3310 -64.0068i which isn't correct.