Patrick_66
Member level 3

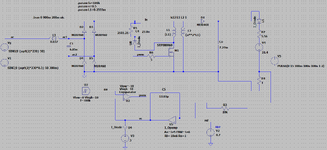
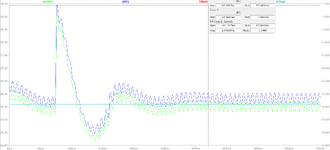
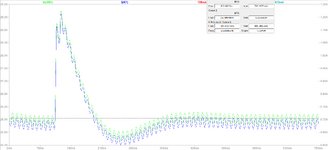
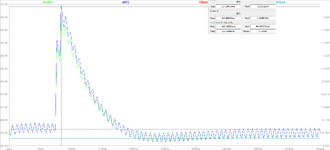
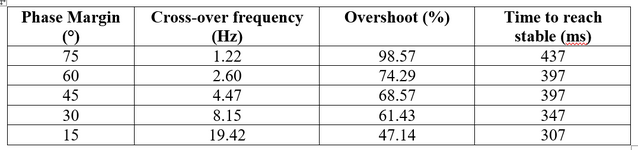
Hello everyone, I'm currently building an LED driver using type one compensation and I simulated the output current with different phase margins and cross-over frequencies to study the response of the system. The result that I got is when the phase margin decreases the cross-over frequency increases and the percentage of overshoot as well as the time to reach transient decreases but the damping increases. Wanted to ask whether this situation is normal? If the result is correct, if possible can you explain why is this situation like this. Thank you in advance and sorry for my ignorance.