zorro
Advanced Member level 4

Ratch,
When one of the two Tau goes to 0 (and the other doesn't) the result is seen immediately from the expression itself: the terms containing the Tau that vanishes disappear from the numerator and from the denominator. Whether it is Tau1=0 or Tau2=0 is irrelevant.
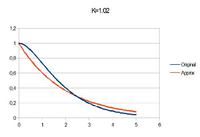
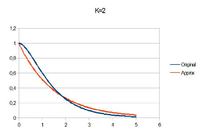
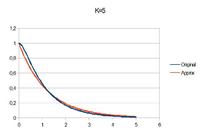
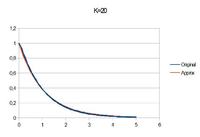
Te book states "This approximation works best when one time constant is significantly bigger that the other". Then shows that it works better for ratio 6.5 (error <7%) than for ratio 1 (error <15%).
The case in which one of the Tau's is 0 is not of interest.
I tried to show that your assertion that the situations tau1<<tau2 and tau2<<tau1 are different is wrong.
Your assertion that the book is wrong is unfair too.
I don't understant why you say that I'm wrong too. Please explain. Thanks
Z
When one of the two Tau goes to 0 (and the other doesn't) the result is seen immediately from the expression itself: the terms containing the Tau that vanishes disappear from the numerator and from the denominator. Whether it is Tau1=0 or Tau2=0 is irrelevant.
Te book states "This approximation works best when one time constant is significantly bigger that the other". Then shows that it works better for ratio 6.5 (error <7%) than for ratio 1 (error <15%).
The case in which one of the Tau's is 0 is not of interest.
I tried to show that your assertion that the situations tau1<<tau2 and tau2<<tau1 are different is wrong.
Your assertion that the book is wrong is unfair too.
Looking over the problem again, I think we are both wrong.
I don't understant why you say that I'm wrong too. Please explain. Thanks
Z