bhl777
Full Member level 6

Hi All, I am testing the data transfer between two wirelss coils.
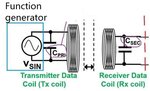
The input sinusoidal signal of the primary coil is from the function generator, whose peak to peak level is 10V and frequency is adjustable between 1MHz to 5MHz.
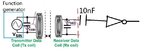
I am using inductive coupling method, to place a cap in parallel with the Tx and Rx coils. This means I can only get resonance at a frequency within the input frequency range. Therefore, Q values at different input frequency shoudl be different.
When I have the distance between two coils fixed (say 1 cm), and two coils aligned with each other, I found the peak to peak amplitude of the sinusoidal signal in Rx are relatively constant (for example, 4V Vpp at Rx when Tx has 10V Vpp) over the entire f range.
If we assume the Vpp at Rx can be determined by L_rx, L_tx, and the coupling factor, can I conclude that the coupling factor is a weak function of Q?
I only know the coupling factor is related to the distance between the coils and the coils' diameter. However, I did not find the equation that relates the coils' coupling factor and the Q. I am not sure if my conclusion based on the exerimental result is correct. Can anyone advise me or refer me to some related papers/books?
Thank you!
The input sinusoidal signal of the primary coil is from the function generator, whose peak to peak level is 10V and frequency is adjustable between 1MHz to 5MHz.

I am using inductive coupling method, to place a cap in parallel with the Tx and Rx coils. This means I can only get resonance at a frequency within the input frequency range. Therefore, Q values at different input frequency shoudl be different.
When I have the distance between two coils fixed (say 1 cm), and two coils aligned with each other, I found the peak to peak amplitude of the sinusoidal signal in Rx are relatively constant (for example, 4V Vpp at Rx when Tx has 10V Vpp) over the entire f range.
If we assume the Vpp at Rx can be determined by L_rx, L_tx, and the coupling factor, can I conclude that the coupling factor is a weak function of Q?
I only know the coupling factor is related to the distance between the coils and the coils' diameter. However, I did not find the equation that relates the coils' coupling factor and the Q. I am not sure if my conclusion based on the exerimental result is correct. Can anyone advise me or refer me to some related papers/books?
Thank you!