rsashwinkumar
Member level 4

Hi all,
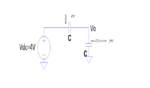
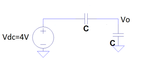
Suppose, I have two capacitors connected in series to act as a divider (same value caps) and i test with a DC input say 4V, what would be the output at the top plate of the cap C2 ? What I thought was (and what i suppose to be right) is that since the capacitors are equi-valued, charge stored across each cap will be the same; so to the left of C1 if positive charges are developed, an equal amount of negative charges will be available on its right plate. At the same time an equal amount of positive charge will be on the top plate of C2, and the bottom plate as is grounded, will have no charge. So effectively, at the output node (which is the top plate of C2), the charges cancel out, 0V will be available at the output.
But, the transfer function of the system (Vout(s)/Vin(s)) = 1/2. So, this states that , output must be 2V
Also, if i apply charge conservation axiom at the output node, initial charge is 0C = Vout*C + (Vout-4)*C [final charge];
This again give me 2V at the output.
So, which of the answers 0V or 2V is right? In either case, what is the wrong with the contradicting proof(s)?
Plz help me out...
Last edited: