pannaguma
Junior Member level 1

- Joined
- Sep 27, 2009
- Messages
- 18
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,281
- Activity points
- 1,441
Hi friends,
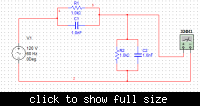
I have been preparing for competitive exams and came across a question on multiple RC circuit time constant derivation...
one particular problem was of the form:
----------R1||C1----------- <------------Vout+
|
|
R2||C2
|
|
---------------------------- <-------------Vout-
input was a DC voltage source I think, assume it parallel to R2||C2...
Now I did a little bit of searching and found this
So I gave a try and followed the same procedure, ie of finding thevenin equivalent of the circuit across the output terminals.
Shorting input voltage source, gives R1, C1, R2, C2 all in parallel with Vout, giving a time constant of [(C1+C2)*(R1*R2/(R1+R2))].
Is this correct? If not can some one please give me hint where I am going wrong?
Thanks for reading, appreciate any sort of help
I have been preparing for competitive exams and came across a question on multiple RC circuit time constant derivation...
one particular problem was of the form:
----------R1||C1----------- <------------Vout+
|
|
R2||C2
|
|
---------------------------- <-------------Vout-
input was a DC voltage source I think, assume it parallel to R2||C2...
Now I did a little bit of searching and found this
So I gave a try and followed the same procedure, ie of finding thevenin equivalent of the circuit across the output terminals.
Shorting input voltage source, gives R1, C1, R2, C2 all in parallel with Vout, giving a time constant of [(C1+C2)*(R1*R2/(R1+R2))].
Is this correct? If not can some one please give me hint where I am going wrong?
Thanks for reading, appreciate any sort of help