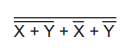[SOLVED] Two's complement: Are there any algebraic 'hidden' properties ?

[andre_luis]

I am studying to make a test for the engineering position in a large company where I live, and I am using a test applied few years ago, and I got stucked with one of the questions, which is:

Let be two numbers X and Y of N bits and consider that the "+" operator refers to a sum of N bits and not to a logical OR operation. Given the bitwise complements of X and Y represented by X_ and Y_, respectively, evaluate the following expression when truncated to N bits:

The first thing that came to mind was to recursively apply the "Two's Complement" rule:



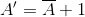
Which rearranged, give:



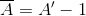
So, replacing each of the last 2 variables at original equation,



Adding the numerals,



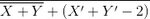
Doing the same for the first 2 variables,



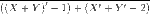
And the same for the upper bar,



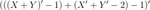
Gathering numerals,



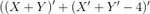
But from here I'm stuck.

I wonder if I'm overlooking some elementary boolean rule.
I'm not sure if I can apply a distributive property to the (') complement operator:



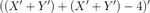
Rearranging,



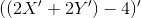
In a different format,



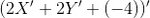
And knowing that the complement means an algebraic signal inversion,



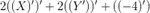
Rearranging,



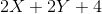
However, correct answer (which I could confirm with random numerals at X and Y) is :

Does anyone have any insight on how to solve that?

 

[albbg]

I've some difficult in finding the error in your derivation, I should read it more carefully. However, I would proceed as follow:

-A=A_+1 from which A_=-A-1. Applying it to your expression we obtain:

-[-(x+y)-1 -x-1 -y-1]-1 = x+y+1+x+1+y+1-1 that is:

2x+2y+2

 

[andre_luis]

Your approach seems more consistent, once you are dealing with the variables only using the algebraic property of signal inversion, whereas I also made the distributive operation - which now I realize that is not applicable here. Thank you, the question surely have been solved.