nahid99
Newbie level 4

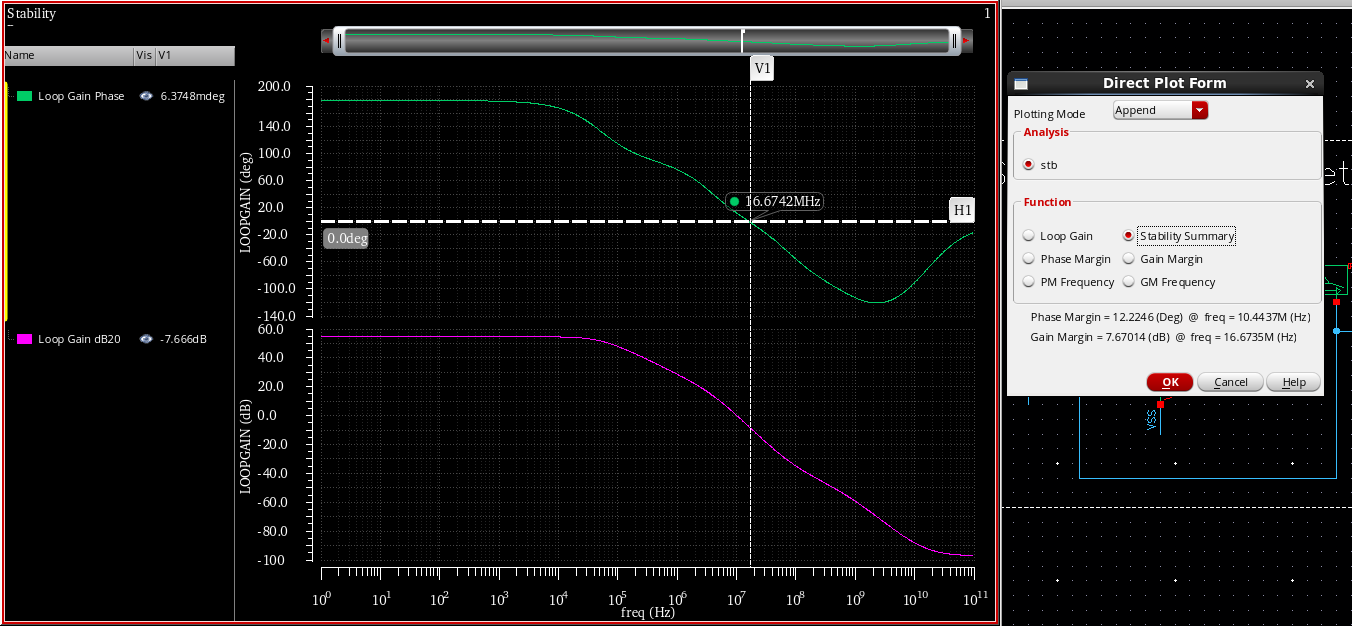
Hi, i am a newbie in Analog IC design. I perform a stability analysis of my Two Stage OTA. As from the textbook the Gain Margin calculated to the -180 phase along with the (0 - Calculated Gain). But in Cadence from the Direct Plot Grom, I get the GM= 7.67dB, when i cross check with the Gain and Phase Plot, the GM calculated in 0dB. Why its calculated in 0 degree rather than -180 degree. Bellow the figure