[SOLVED] Same question. Two different results. Please Help.

[bishshoy007]

For this circuit given in the figure below :


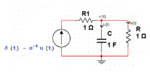
(Click to Enlarge)

Given that the initial voltage \[v(0-) = 4 V\], find out \[{i }_{c }(t)\], i.e current through the capacitor for \[0^- < t < \infty\] .

I have tried out the sum in two ways. First, I found out a differential node equation in \[v(t)\], i.e

\[v'[t] + v[t] = \delta (t)-e^{-t}u(t)\]

and solve it to get :

\[ v(t) = \left(5e^{-t}-t e^{-t}\right)u(t)\],

where \[u(t)\] is the UnitStep function. Also the required initial conditions was obtained as \[v(0+) = 5 V\], which I believe is perfectly all right. Next to find out \[{i}_{c}(t)\], I use :

\[{i}_{c}(t) = C \frac{\mathrm{d} v(t) }{\mathrm{d} t } = 5\delta (t) - 6e^{-t}u(t) + t e^{-t}u(t) \]

Now in procedure 2, which was done by a friend of mine, he found out \[{i}_{c}(t)\] by writing

\[\delta (t)-e^{-t}u(t) = i_c(t)+i_R(t)\]

and
\[i_R(t)=\int _{0^-}^ti_c(t)dt+v(0-)\].

Combining both equations and transforming into the Laplace equivalent, he arrived at

\[I_c(s) = \frac{s^2-4s-4}{(s+1)^2} \]

whose inverse would be

\[i_c(t) = \delta (t) - 6e^{-t}u(t) + t e^{-t}u(t) \].

Here lies the problem. The coefficient of the delta functions do not match.

So the two answers are different. :-? Where is the mistake ? I have tried the problem several times from scratch but still I am unable to find it out and this problem is bugging my sleep for many days. Please help me. I repeat the problem is that in the answers the strengths of the delta functions or the coefficients of the delta functions are different.

 

[bishshoy007]

alas, nobody there to help me out ! :-(

 

[_Eduardo_]

alas, nobody there to help me out ! :-(

? ? ? Only one day. Are you...Anxious?


\[ v(t) = \left(5e^{-t}-t e^{-t}\right)u(t)\] isn't correct because v(0-) is 0 instead 4 and you derive u(t) at 0.

You should write something like this \[ v(t) = 4 u(-t) + \left(5e^{-t}-t e^{-t}\right)u(t)\]

whose derivative coincides with the other result.

 

[bishshoy007]

? ? ? Only one day. Are you...Anxious?


\[ v(t) = \left(5e^{-t}-t e^{-t}\right)u(t)\] isn't correct because v(0-) is 0 instead 4 and you derive u(t) at 0.

You should write something like this \[ v(t) = 4 u(-t) + \left(5e^{-t}-t e^{-t}\right)u(t)\]

whose derivative coincides with the other result.

I cannot site the reason as to how we can write v(t) like that.
If I convert the circuit into Laplace domain and evaluate for \[V (s) = (5 s + 4)/(s + 1)^2\]
then I get \[v(t)=-e^{-t} (-5+t)u(t)\] which is same as that obtained from the differential equation.

- - - Updated - - -

Some further analysis shows that during laplace transform, we do both
L[u(t)] = 1/s
and
L[1] = 1/s

and hence the the inital voltage on the capacitor gets modeled as v(0-)/s whose inverse would be v(0-) u(t) ?? And hence in the inverse transform all information about t<0 is lost !

Can you point me in the right direction ?

- - - Updated - - -

I have used Mathematica to solve for

v'[t] + v[t] = DiracDelta[t] , given v[0-] = 4

and the output is

Exp[-t] (4 + u[t])

which correctly determines the value at t = 0- as 4 !

But the differential equation if solved by laplace transform, a little mathematics shows

V = 5/(s+1), whole inverse laplace mathematica gives as

v[t] = 5 Exp[-t] !!!

Somebody please help !

 

[albbg]

Eduardo is right. In 0+ you have a pulse to +5V, but starting from V(0-)=0 since you used u(t) that is 0 from 0- down to infinity

From the problem conditions, instead, in 0- you must have 4V, then the amplitude of the pulse is given by V(0+)-V(0-) = 5-4 = 1; this is the coefficient of the dirac pulse in 0.