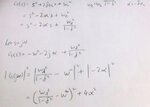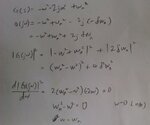promach
Advanced Member level 4

Bode Plot
1) Why the gain plot |G(jw)| drops and then increases for conjugate zeroes ?
2) Why the gain plot |G(jw)| increases and then drops for conjugate poles ?
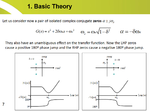
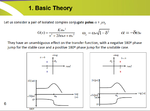
Nyqust Plot
3) For Figure 9-18(B), could anyone explain in a bit more details than the book as on how to obtain the Nyquist plot pattern ?

1) Why the gain plot |G(jw)| drops and then increases for conjugate zeroes ?
2) Why the gain plot |G(jw)| increases and then drops for conjugate poles ?


Nyqust Plot
3) For Figure 9-18(B), could anyone explain in a bit more details than the book as on how to obtain the Nyquist plot pattern ?