trobe.
Newbie level 4

Hey guys,
I'm doing a project on RF and I ran into a problem. I hope you can take the time to try and answer some of my questions.
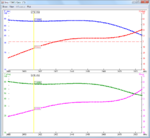
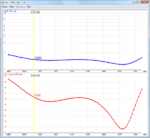
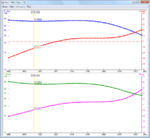
I build a 15dBi Yagi antenna for wifi purposes and I have done some measurements which include plotting the S11. But now I want to turn these values into complex impedance (read: Zin). The formula to do this is: Zin = [(1 + S11) / (1 - S11)] * Z0, in which Z0 is 50 ohm. Now, as I tried this formula out on my theoretical values in my 4Nec2 design I found something strange. If I'd take a theoretical S11 value at a certain frequency it wouldn't match the theoretical Zin at the same frequency. Example:
S11 = -13.6 dB @2416MHz
Z0 = 50 ohm
gives => Zin = -43.2 ohm
whilst the theoretic value of Zin is 73.8 ohm. (see attachments)
What am I doing wrong here? Perhaps the Refl. Coef =/= S11?
I would be really grateful if you'd take the time to answer my question.
Greetings from Holland