viperpaki007
Full Member level 5

Hi,
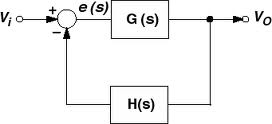
In most of cases, a circuit is stable when it does not have any positive feedback. This means that the phase shift of the feedback path is not 360 degrees. Then why in the phase margin definition 180 degree is used to check the stability. I believe that phase margin should be measured with 360 degree reference because at 360 degree phase shift, positive feedback occurs, which causes stability problems.
In most of cases, a circuit is stable when it does not have any positive feedback. This means that the phase shift of the feedback path is not 360 degrees. Then why in the phase margin definition 180 degree is used to check the stability. I believe that phase margin should be measured with 360 degree reference because at 360 degree phase shift, positive feedback occurs, which causes stability problems.