Georgy.Moshkin
Full Member level 5

Large patch antenna arrays often use 3-way splits in the feeding network. I want to share a simple explanation on how to perform unequal splits if one needs to implement weighting of subarrays.
Here is how you can do it:
For example, if the input port impedance is Z0=25 Ohm
and we need to divide the power between to achieve 50%, 30% 20% division ratio, then impedances for these ports can be calculated as
Z1 = Z0 / k1 = Z0 / 0.5 = 50 Ohm
Z2 = Z0 / k2 = Z0 / 0.3 = 83.33 Ohm
Z3 = Z0 / k3 = Z0 / 0.2 = 125 Ohm
where power division ratios calculated as
k1 = 50% / 100% = 0.5
k2 = 30% / 100% = 0.3
k3 = 20% / 100% = 0.2
and k1+k2+k3 = 0.5+0.3+0.2 = 1.0
and ideal transmission values are
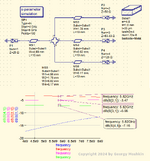
S21 = 10*Log10(k1) = 10*Log10(0.5) = -3 dB
S31 = 10*Log10(k2) = 10*Log10(0.3) = -5.23 dB
S41 = 10*Log10(k3) = 10*Log10(0.2) = -6.99 dB
Next, you can use microstrip line calculator to find line width for each port at some frequency. For example, for a 1.0mm thick substrate with Er=4.8 at 5.8GHz line widths are:
w0 = 4.98 mm (25 Ohm) - input port
w1 = 1.78 mm (50 Ohm)
w2 = 0.62 mm (83.33 Ohm)
w3 = 0.17 mm (125 Ohm)
Such 4-way junction is sometimes called a "microstrip cross". In most cases widths at some ports become too narrow, such as 0.01mm. In such cases simply replace this output line port with quarterwave transformer to a lower impedance. For example, if minimal manufacturable line width is 0.3mm, then w3 = 0.17 mm can't be used in final design. Therefore, we can replace 0.17mm line with a quarterwave transformer w3=0.3mm. From microstrip calculator, impedance of 0.3mm wide microstrip line is 107.2 Ohm.
This means that Ztransformer=sqrt(Z3*Znew)=107.2 Ohm
Znew=107.2^2 / Z3 = 91.93 Ohm
and 0.17mm-wide line at port 3 can be replaced with a quarterwave transformer with dimensions W=0.3mm, L=7.2mm, which is followed by a Znew line with width W=0.48mm. In other words, we replaced port 3 with a quarterwave transformer Ztransformer = Sqrt(91.93*125)=107.2 Ohm to eliminate narrow 0.17mm section.
Another way thinking of this division is to use "virtual impedance" idea. Assume that we need 50%, 30% 20% division ratio, so our power division coefficients are
k1=0.5
k2=0.3
k3=0.2
Instead of 4-port device, we can first consider 3-port device and perform 50% division:
k1=k2=0.5
Z1 = Z0 / 0.5 = 50 Ohm
Z2 = Z0 / 0.5 = 50 Ohm
Now we can use Z2 as a virtual impedance and divide it again.
We know that Z2 receives only 50% of power, because k2+k3 = 0.3+0.2 = 0.5. And we can split power coming into "virtual" (or invisible/having zero length) port Z2 again by using new power ratios.
m1 = k2/(k2+k3) = 0.3/0.5 = 0.6
m2 = k3/(k2+k3) = 0.2/0.5 = 0.4
Z2 / m1 = 50 / 0.6 = 83.33 Ohm
Z2 / m2 = 50 / 0.4 = 125 Ohm
As you can see, calculated port impedances have the same value if calculated using virtual impedance principle.
While I think that this is correct approach, I would be glad if someone comments or have any related questions. For instance, I want to confirm if using "virtual impedance" terminology is appropriate when teaching this topic to my students. Is there a better term for zero-length elements?
Here is how you can do it:
For example, if the input port impedance is Z0=25 Ohm
and we need to divide the power between to achieve 50%, 30% 20% division ratio, then impedances for these ports can be calculated as
Z1 = Z0 / k1 = Z0 / 0.5 = 50 Ohm
Z2 = Z0 / k2 = Z0 / 0.3 = 83.33 Ohm
Z3 = Z0 / k3 = Z0 / 0.2 = 125 Ohm
where power division ratios calculated as
k1 = 50% / 100% = 0.5
k2 = 30% / 100% = 0.3
k3 = 20% / 100% = 0.2
and k1+k2+k3 = 0.5+0.3+0.2 = 1.0
and ideal transmission values are
S21 = 10*Log10(k1) = 10*Log10(0.5) = -3 dB
S31 = 10*Log10(k2) = 10*Log10(0.3) = -5.23 dB
S41 = 10*Log10(k3) = 10*Log10(0.2) = -6.99 dB
Next, you can use microstrip line calculator to find line width for each port at some frequency. For example, for a 1.0mm thick substrate with Er=4.8 at 5.8GHz line widths are:
w0 = 4.98 mm (25 Ohm) - input port
w1 = 1.78 mm (50 Ohm)
w2 = 0.62 mm (83.33 Ohm)
w3 = 0.17 mm (125 Ohm)
Such 4-way junction is sometimes called a "microstrip cross". In most cases widths at some ports become too narrow, such as 0.01mm. In such cases simply replace this output line port with quarterwave transformer to a lower impedance. For example, if minimal manufacturable line width is 0.3mm, then w3 = 0.17 mm can't be used in final design. Therefore, we can replace 0.17mm line with a quarterwave transformer w3=0.3mm. From microstrip calculator, impedance of 0.3mm wide microstrip line is 107.2 Ohm.
This means that Ztransformer=sqrt(Z3*Znew)=107.2 Ohm
Znew=107.2^2 / Z3 = 91.93 Ohm
and 0.17mm-wide line at port 3 can be replaced with a quarterwave transformer with dimensions W=0.3mm, L=7.2mm, which is followed by a Znew line with width W=0.48mm. In other words, we replaced port 3 with a quarterwave transformer Ztransformer = Sqrt(91.93*125)=107.2 Ohm to eliminate narrow 0.17mm section.
Another way thinking of this division is to use "virtual impedance" idea. Assume that we need 50%, 30% 20% division ratio, so our power division coefficients are
k1=0.5
k2=0.3
k3=0.2
Instead of 4-port device, we can first consider 3-port device and perform 50% division:
k1=k2=0.5
Z1 = Z0 / 0.5 = 50 Ohm
Z2 = Z0 / 0.5 = 50 Ohm
Now we can use Z2 as a virtual impedance and divide it again.
We know that Z2 receives only 50% of power, because k2+k3 = 0.3+0.2 = 0.5. And we can split power coming into "virtual" (or invisible/having zero length) port Z2 again by using new power ratios.
m1 = k2/(k2+k3) = 0.3/0.5 = 0.6
m2 = k3/(k2+k3) = 0.2/0.5 = 0.4
Z2 / m1 = 50 / 0.6 = 83.33 Ohm
Z2 / m2 = 50 / 0.4 = 125 Ohm
As you can see, calculated port impedances have the same value if calculated using virtual impedance principle.
While I think that this is correct approach, I would be glad if someone comments or have any related questions. For instance, I want to confirm if using "virtual impedance" terminology is appropriate when teaching this topic to my students. Is there a better term for zero-length elements?