chiques
Full Member level 3

- Joined
- Nov 21, 2007
- Messages
- 170
- Helped
- 2
- Reputation
- 4
- Reaction score
- 2
- Trophy points
- 1,298
- Location
- California
- Activity points
- 2,556
I went through this tutorial which seems fairly straight forward: Parallel Resonant Circuit Math

My question is, how does this change when I switch over to a source that has a 50 ohm impedance?
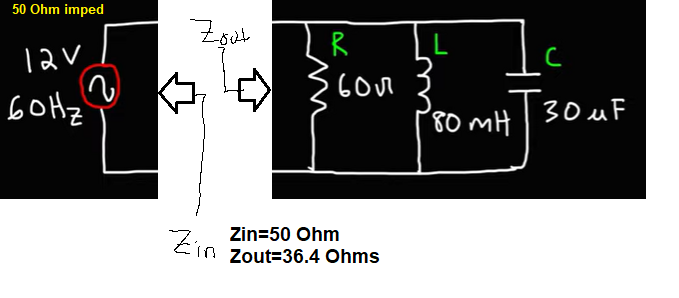
Zin = 50 Ohms
Zout = 36.4 Ohms
My question is, how does this change when I switch over to a source that has a 50 ohm impedance?
Zin = 50 Ohms
Zout = 36.4 Ohms


