carbon9
Member level 3

Nano device question
Hi dears,
I'm following the book of Datta named "Quantum Transport: Atom to Transistor". But just at the beginning, I'm confused a bit
In the book, at chapter 1, there are some equations given for the current in nanotransistors.
Specially, an equation for a system with density of states D(E) sandwiched between contacts having Fermi functions f1(E) and f2(E) is given by
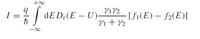
Also, in order to make some calculations, author have given MATLAB files to calculate these formulas. In all of the MATLAB formulas, current is calculated as:
for iV=1:IV
mu1=ep+VV(iV);
mu2=mu1;
f1=1./(1+exp((E-mu1)/kT1));
f2=1./(1+exp((E-mu2)/kT2));
D=(g./(2*pi))./(((E-ep).^2)+((g./2).^2));
D=D./(dE*sum(D));
I(iV)=dE*2*I0*(sum(D.*(f1-f2).*g1.*g2./g));
end
where
hbar=1.055e-34;
q=1.602e-19;
I0=q*q/hbar;
So, as I understand, he calculates the formula in MATLAB as if the multiply factor of the formula is q^2/hbar not q/hbar which he shows in the chapter. Could you please give any idea on this?
With regards,
Hi dears,
I'm following the book of Datta named "Quantum Transport: Atom to Transistor". But just at the beginning, I'm confused a bit
In the book, at chapter 1, there are some equations given for the current in nanotransistors.
Specially, an equation for a system with density of states D(E) sandwiched between contacts having Fermi functions f1(E) and f2(E) is given by
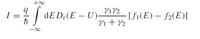
Also, in order to make some calculations, author have given MATLAB files to calculate these formulas. In all of the MATLAB formulas, current is calculated as:
for iV=1:IV
mu1=ep+VV(iV);
mu2=mu1;
f1=1./(1+exp((E-mu1)/kT1));
f2=1./(1+exp((E-mu2)/kT2));
D=(g./(2*pi))./(((E-ep).^2)+((g./2).^2));
D=D./(dE*sum(D));
I(iV)=dE*2*I0*(sum(D.*(f1-f2).*g1.*g2./g));
end
where
hbar=1.055e-34;
q=1.602e-19;
I0=q*q/hbar;
So, as I understand, he calculates the formula in MATLAB as if the multiply factor of the formula is q^2/hbar not q/hbar which he shows in the chapter. Could you please give any idea on this?
With regards,
