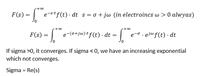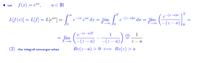[moved] Laplace transform, convergence, Basic circuit theory question.

[ammar_kurd]

Hi guys,

I was reading in a circuit theory book, and after the definition of the Laplace transform it says how important is that the integral converges therefore the function f(t) defined for t > 0 and is zero for t <= 0. Then it continuous and I quote the book here,

"Accordingly, for most of the functions encountered in electrical engineering, convergence is ensured by imposing the condition that the real part of s be positive, i.e., that Re > 0 "

My question is why the real part only is to be positive?

 

[CataM]

By definition, Laplace transform exists only when that integral converges.

That was for signals that not affect the exponential (signals from real life), but If we talk mathematically here is an example that shows that not always Re(s)>0, only if the signal do not affect the exponential as said above.

- - - Updated - - -



NOTE: here "z" is used as "s". Do not confuse it with "z" from z Transform.