wfg42438
Member level 3

- Joined
- Jun 29, 2015
- Messages
- 54
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 6
- Location
- California
- Activity points
- 620
Hello, I am trying to design a frequency synthesizer with the use of the CD4046B IC which is a PLL. Based on some research I have done I see that this is possible with the addition of a divide by N counter in the feedback loop between the VCO and phase comparator input. Before doing this there are resistors and capacitors that have to be designed for, they depend on the frequency ranges you decide to work with.
This design will be used as a subsystem in a project but in order to keep things simple let me list the relevant specs to PLL only. This circuit will simulate a speedometer, based on the frequency of the input signal we wish to convert this to MPH reading.
The specification given to start off with is:
1) The input is a pulse of 0.5V magnitude occurring every two revolutions
2) 2500 Rev/ Min = 60MPH -------- 1250 Pulses/min = 60 MPH
Based on this information I see the following:
X * 1250 Pulses/min = 60 MPH therefore ------ X = 2.88 MPH/Freq_Pulse
Now let’s assume the input has been ran through a Schmitt trigger which has cleaned up the signal (giving it logic levels of 0V (Low) and 5V (High State)) with the same frequency as our original input.
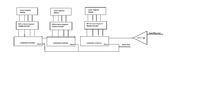
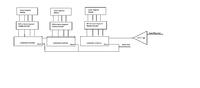
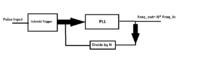
So the idea here is to take the signal at the output of the Schmitt trigger and input that into our PLL. Now if the PLL is designed appropriately we can convert the incoming frequency to MPH by multiplying the input frequency by a value N (Please see attached block diagram). Now I’m assuming multiplying by 2.88 will not be easy therefore I think the next best thing we will need to multiply by 288. I’m assuming once I move on to the counter it can be manipulated one more time to get us the correct N multiplier however lets hold off on that and focus on the PLL design for now.
Based on the data sheet I have found the following:
If VDD=5V, N=288
For the VCO let’s see what the lowest and highest frequencies we will produce:
Let the lowest speed we can display be 10 MPH & the highest be 99.9 MPH
Therefore: fmin= (10 MPH)/( 2.88) )* 288 = 999.99 Hz --- let fmin=1kHz
Fmax= (99.9 MPH)/ (2.88))* 288= 9.999 kHz - let Fmax=10kHz
Using the data sheet limits and graphs we arrive at:
Fmax/fsmin = 10 , f_center= 5.5 kHz & R2/R1 = 20
Next letting R1= 10k R2 =200k, C1=6800pF
For the Filter it was found: R4=2.7k, C2=3.9 uF, , & R3=6.2k
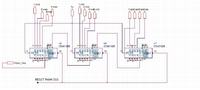
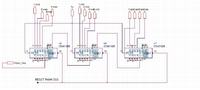
Now under the assumption that the external Caps and resistors R1-R4 & C1-C2 are chosen correctly how do I go about introducing the divide by N block into the feedback loop?
https://www.mouser.com/ds/2/405/cd4046b-439718.pdf
- - - Updated - - -
Adding the Block Diagram:
This design will be used as a subsystem in a project but in order to keep things simple let me list the relevant specs to PLL only. This circuit will simulate a speedometer, based on the frequency of the input signal we wish to convert this to MPH reading.
The specification given to start off with is:
1) The input is a pulse of 0.5V magnitude occurring every two revolutions
2) 2500 Rev/ Min = 60MPH -------- 1250 Pulses/min = 60 MPH
Based on this information I see the following:
X * 1250 Pulses/min = 60 MPH therefore ------ X = 2.88 MPH/Freq_Pulse
Now let’s assume the input has been ran through a Schmitt trigger which has cleaned up the signal (giving it logic levels of 0V (Low) and 5V (High State)) with the same frequency as our original input.
So the idea here is to take the signal at the output of the Schmitt trigger and input that into our PLL. Now if the PLL is designed appropriately we can convert the incoming frequency to MPH by multiplying the input frequency by a value N (Please see attached block diagram). Now I’m assuming multiplying by 2.88 will not be easy therefore I think the next best thing we will need to multiply by 288. I’m assuming once I move on to the counter it can be manipulated one more time to get us the correct N multiplier however lets hold off on that and focus on the PLL design for now.
Based on the data sheet I have found the following:
If VDD=5V, N=288
For the VCO let’s see what the lowest and highest frequencies we will produce:
Let the lowest speed we can display be 10 MPH & the highest be 99.9 MPH
Therefore: fmin= (10 MPH)/( 2.88) )* 288 = 999.99 Hz --- let fmin=1kHz
Fmax= (99.9 MPH)/ (2.88))* 288= 9.999 kHz - let Fmax=10kHz
Using the data sheet limits and graphs we arrive at:
Fmax/fsmin = 10 , f_center= 5.5 kHz & R2/R1 = 20
Next letting R1= 10k R2 =200k, C1=6800pF
For the Filter it was found: R4=2.7k, C2=3.9 uF, , & R3=6.2k
Now under the assumption that the external Caps and resistors R1-R4 & C1-C2 are chosen correctly how do I go about introducing the divide by N block into the feedback loop?
https://www.mouser.com/ds/2/405/cd4046b-439718.pdf
- - - Updated - - -
Adding the Block Diagram: