Motor power calculation for Swing Gate

[kanni1303]

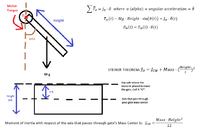
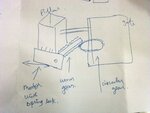
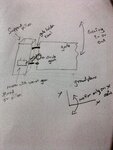
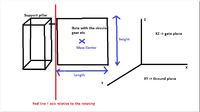
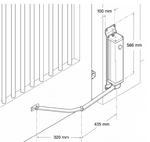
Hi, We are designing RF controlled swing gate open/close controller, we finished the controller part and tested with proto, but we don't know how to calculate power rating for the actual Motor to drive the Swing Gate of about 10ft long, 8ft height and 350KGs. Help me to calculate the power required to swing the gate. for moving the gate I can use f=ma expression and after that I may derive the power depending type of motor, but for swing I don't know how...

 

[c_mitra]

Use the angular momentum calculation. You just need to tell us how much time you expect for the door to open fully (90 degree open). In this calculation, use 45 degree as acceleration and remaining 45 degree for deceleration. Calculate the energy when the door is half open and it has the max angular velocity. Use the energy 1/2 * I * w^2 (I=moment of inertia * w^2 where w is the angular velocity). w=0 at t=0; and at t/2 w=a*(t/2) where a is the torque. Rest should be easy, I guess.

 

[BradtheRad]

A great deal depends on the pivot, hinge, and bearings. The gate must be easy to get moving. This may even be more important than its length, height, weight.

Use ball bearings if possible. I can imagine a gate of your dimensions needing automotive wheel bearings.

About motor power... probably the same rating that pulls a motorboat up onto a trailer. Do not yank too close to the pivot. Yank at a foot or two distance.

Pulling the gate in one direction is easy. To make it go the other direction, you may want to install a counterweight, or, make the gate off-vertical, or whatever looks the smartest way.

- - - Updated - - -

My reply is off the top of my head and it's probably off in other ways as well. Have you looked in catalogs of such equipment to find ideas?

 

[c_mitra]

You can use a small motor with lots of gears to open the door slowly... Or, use a jumbo motor that opens it fast... When the door is coming to a stop (second half of the travel), it is dumping its energy onto the motor and the motor is being driven, rather than...

You should also think of brakes and clutches...

 

[kanni1303]

thank you all for the inputs.
@c_mitra, I can't use angular momentum formulae here, since the actual force applied to the gate is not angular, your formulae works when riding in a bike and taking curve so we can use angular momentum
@BradtheRad
unfortunatly i have to fix yank near the pivot since the surface is not flat as I can use trail to move, also what is the need of counterweight to revrse i can simple reverse the motor rotation in open and close? pls explain
@c_mitra
yes i planned to use worm gear fixed on motor and circular gear fixed on gate, since this setup produces more torque. also for breaking it will be easy to stop the motor with this setup.

 

[BradtheRad]

what is the need of counterweight to revrse i can simple reverse the motor rotation in open and close? pls explain

Then there is no need for a counterweight in your system. Sometimes a counterweight is useful because it allows a smaller motor to be used.

Your gate is massive. It is wise for you to include a clutch somewhere. You need to relieve strain on your system at such times when:

* As the gate reaches the ends of its travel
* If wind is blowing against the gate
* Any irregular motion of the gate during opening or closing

 

[CataM]

Help me to calculate the power required to swing the gate. for moving the gate I can use f=ma expression and after that I may derive the power depending type of motor, but for swing I don't know how...

What I am going to show you is an approximation since I think the weight is not applied in it's center mass, because the mass is distributed homogeneously across all the gate.

I have used the fundamental equation of the rotational dynamic which is like the Newton's 2nd law for Forces (Sum of applied forces=mass·acceleration). Here is: Sum of applied torques to the gate=inertia moment of the mass respected to the moving axis (in our case I have called it "O") · angular acceleration of the gate.

NOTE 1:theta with 2 points over it which means second derivative of theta with respect the time 2 times. (means the angular acceleration)

NOTE 2: If you do not want angular acceleration => theta with 2 points = 0

NOTE 3: Pm=motor power and Tm=motor torque.

NOTE 4: Note that I have placed the general vectorial equation of the rotational dynamics but 1 line below appears ....-Mg·height·sin.... which is a scalar equation

 

[FvM]

I can't use angular momentum formulae here, since the actual force applied to the gate is not angular

That's an unfounded claim unless you show a drawing.

 

[CataM]

Mistake found (sorry):
In the photo it says this: Tm(t)-Mg·Height·sin(theta(t))=etc

Change "Height" with "Height/2" so the equation should be:
Tm(t)-Mg·(Height/2)·sin(theta(t))=etc..

Sorry again !

 

[kanni1303]

@BradtheRad,
for that I have a plan to slide the motor with worm gear assembly to detach from gate so that it can be operated manually (will be helpfull during power fail or catastrophe)
@CataM
sorry I think you designed for lift gate, my gate is swing one which the gate will swing inside or outside(open close) so the mass is distributed and gravity is negligible (but whereas friction, shearing, wind and other resistance may be included) the mass movement is not against the gravity (ie theta will be 0 or near zero)
@FvM
PFA


the design is, motor with worm gear setup will be fixed on the supporting pillar and it will adjusted so that detachable from gate. A circular gear is place in the gate now worm gear will rotate the circular to rotate the gate and the gate will swing to open and close.

 

[BradtheRad]

The theory is good, of course. However you should expect the unexpected. It's a good idea to 'over-engineer' your mechanism. You are looking to achieve a balance between rigidity and 'give'. If you do not build in some 'give' then you will need to build in repairability.

* Angular momentum was brought up. There is a time when this will be a factor, when the gate is in motion, and the motor stops suddenly. Angular momentum (inertia) will carry the gate's weight (800 lbs) moving another inch or so, and then exert a lot of force against your mechanism.

* Or one day someone (child or grownup) will try to 'hurry up' the gate, and push on it, and cause enormous force on be exerted on your motor and its mounts.

Your diagram proposes to inscribe (grind) large gear teeth into your gatepost. This appears to be only an inch or two from your pivot axis. I believe you'll encounter extreme problems. The principle of the lever is at work here. It may be possible to calculate the forces involved, although experimentation is the only way you can find out. I suggest you run tests, where you push against the gate at various distances from its pivot axis. Measure the force required to move it, and measure the force which the gate exerts.

- - - Updated - - -

That is, measure the force which the gate exerts back at you, when someone pushes against the furthest end of the gate.

 

[CataM]

A circular gear is place in the gate now worm gear will rotate the circular to rotate the gate and the gate will swing to open and close.

In your 3rd picture you are saying this: "motion only on X axis"... Did you mean circular only on XY plane ?



Of course calculations are only an approximation.. Experience and real measurements have the last words.

If moving only on XY plane then simplifies things. Because of those gears Power motor used to create the torque is not the one that will see the gate.

Inertia moment changes then: Jcm=1/12*(Mass*length^2) and then the Inertia moment relative to the rotation (red line) applying Steiner's Theorem is Jo=Jcm+Mass*(Length/2)^2.

After you have calculated the Torque at the gate, transform it to find the torque of the motor and then find the power of the motor.

Now the equation is like this: Torque at the gate=Jo*angular acceleration+B·angular speed (B=losses)

NOTE: About that "B", that is what theory says... real life is other stuff to find them. I do not know how to model the losses (I mean, what is an appropriate value for "B"...)

- - - Updated - - -

It may be possible to calculate the forces involved, although experimentation is the only way you can find out. I suggest you run tests, where you push against the gate at various distances from its pivot axis. Measure the force required to move it, and measure the force which the gate exerts.

Yes, and you also can do that to find wind's force (to take an extreme case, go to some place where are heavy winds and measure it's force or even it's torque).

 

[FvM]

I don't believe that the worm gear idea will work well due to the unstable gate bearing. Technical gate drives that I know are using lever arms or push rods. The drives are rated for specific gate width and weight.

 

[Warpspeed]

Have you considered using simple hydraulics ?

Something like a reversible electric gear pump and double acting ram.

 

[c_mitra]

Till you tell us the time you need to open the gate, power cannot be calculated. A small motor with gears, can move a heavy gate but will take very long time. The gate, it appears from your drawings, is not supported at the open end- all the weight is borne by the hinges. Mechanically, this is equivalent to a cantilever. Your gate is 10 ft long and the center of gravity will be somewhere close to 5 ft. You are applying force close to 1.5 distance from the hinges.

For a frictionless system, no work is to be done to open or close the gate. All the energy is used in the friction at the hinges. The gate is in neutral equilibrium at all positions. The motor power needed is not much but must be conservatively rated (depends on the speed of opening and closing).

 

[kanni1303]

@FvM and @Warpspeed
I can't use that idea, since I want open on both side (180 degrees), in hydrolics or ARM method only 90degrees possible
@c_mitra
I am working on practical device so there is no point in frictionless case. Also for calculating the energy only we need Time. to calculate power no need of time (Also small power motor cannot move more weight that is greater than its power instead running long time will burn the motor)

 

[FvM]

I can't use that idea, since I want open on both side (180 degrees), in hydrolics or ARM method only 90degrees possible

There's surely a solution but it requires profound mechanical engineering. The motor power will be known after you finished the drive design.