Junus2012
Advanced Member level 5

Dear friends,
below is the image of the 4th order sallen key LPF, I have a deviation from the Butterworth approximation as it is noticeable.
While in ideal butterworth the cutoff frequency is calculated at the - dB frequency, but what about this case ?
Also could you please help me how to calculate the resulted Q from the response?
Thank you
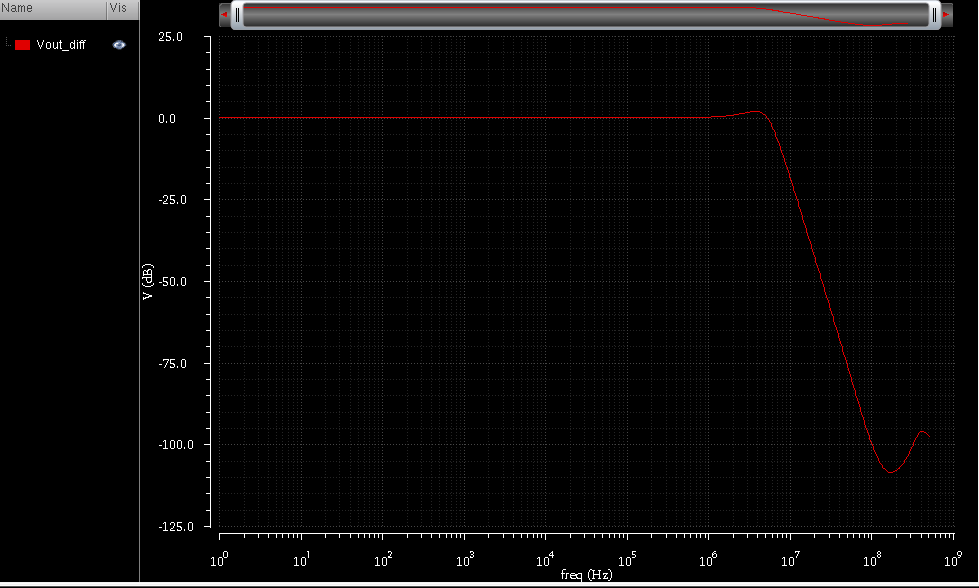
below is the image of the 4th order sallen key LPF, I have a deviation from the Butterworth approximation as it is noticeable.
While in ideal butterworth the cutoff frequency is calculated at the - dB frequency, but what about this case ?
Also could you please help me how to calculate the resulted Q from the response?
Thank you


