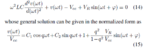MATLAB funstion "dsolve" gives complex terms

[mmr123]

I am facing problem in using dsolve. The solution it gives has complex terms but my expected answer is completely real. Attached is the picture of the differential equation and its general solution which I am trying to get using MATLAB

​

Here is my code:

syms Vs(x) w l C phi Vcc Vr
q= 1/(w*sqrt(l*C));
ode = w*w*l*C*diff(Vs,x,2)+Vs==Vcc-Vr*sin(x+phi); % non-homogenous second order DE
Vs = dsolve(ode,x,'IgnoreAnalyticConstraints',1);
Vs= simplify(Vs);
pretty(Vs)

This gives the solution:

Vr sin(phi + x) - Vcc - C5 exp(#1) - C6 exp(-#1) + C Vcc l (w^2) + C C5 l (w^2) exp(#1) + C C6 l (w^2) exp(-#1)
----------------------------------------------------------------------------------------------------------
C l (w^2) - 1
x sqrt(-C l)
#1 == ------------
C l w

which after some simplication with hand gives the following:

Vs(x)= (q^2/(1-q^2))*Vr*Sin(phi+x)-Vcc-C5*cosqx-i*C5*Sinqx-C6*cosqx+i*C6*sinqx

Clearly we have imaginary terms in terms in it.

If the DE is solved by hand it gives the following:

V(x)= C1*cos(q*x) + C2*sin(q*x) + Vcc + (q^2)/(1-q^2)*Vr*sin(phi+x)

The expected solution as calculated by hand does not contain any imaginary part. Moreover, the solution given by dsolve does not fully match with the expected one. I don't undestand where I am doing wrong. Kindly help me to debug this.

 

[wwfeldman]

i am not a user of MATLAB

however:
in your "equation" ode = , the ode is a function of x, but x is wt.
did do you tell MATLAB that x = wt?

i used MATHEMATICA a few years ago to fit a sinusoidal curve
i also got imaginary answers when i did not expect them
first, the imaginary parts were very small, so it didn't matter (? not quite sure about that, even then)
second, i squared and square rooted one term - which removed a minus sign, but did not change the
appropriateness of the fit equation, and the imaginary terms disappeared.

i do not expect this makes any difference:
the text you posted had everything on the left side = 0
you gave MATLAB had left side == right side

as a user of MATLAB, you can determine is any of these items makes a difference or not