gbugh
Member level 5

- Joined
- Mar 15, 2013
- Messages
- 81
- Helped
- 1
- Reputation
- 2
- Reaction score
- 1
- Trophy points
- 1,288
- Location
- Fort Worth, Texas
- Activity points
- 2,234
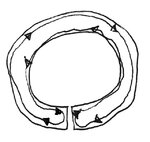
I came across a patent for a thick wall copper tube with an electrical gap in its side so there won't be current flow. Does this type of design actually work for concentrating flux? Like this: https://patents.google.com/patent/US6720855B2/en
If this flux conduit doesn't work, how do people usually create an area of more concentrated flux inside a coil?
If it does work, how does it work when no current flows in the thick copper tube?
Thanks, George
If this flux conduit doesn't work, how do people usually create an area of more concentrated flux inside a coil?
If it does work, how does it work when no current flows in the thick copper tube?
Thanks, George