Location of at Equilibrium
- Thread starter kakar133
- Start date
- Status
- Not open for further replies.
albbg
Advanced Member level 4

OK, we are speaking here of instable equilibrium, that means the sum of forces on Q2 will be zero statically in the first time instant then the system will evolve.
First of all the add charge Q3 must stay on the line where Q1 and Q2 are placed, otherwise a non compesated force will be created. We can note that, in this case, the line connecting Q1 and Q2 is y=x.
If we place the charge on the first quadrant, then Q2 will be repulsed by Q1 and attracted by Q3 then the two forces will be directed on the same way so their sum will not be zero. If instead we place the charge on the third quadrant, Q2 will be replused by Q1 and attracted by Q3 with the two forces directed in opposite direction. Then this is our case.

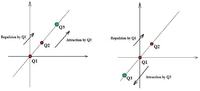
In order to calculate the position we have to know that the force between two charges "Qa" and "Qb" place at a distance "dab" is proportional to:
f\[\propto\]Qa*Qb/dab2
the distance between Q1 and Q2 is d12=sqrt((0-1)2+(0-1)2)=sqrt(2) then f12\[\propto\]Q1*Q2/sqrt(2)
now the distance Q2 and Q3 is d23=sqrt((x-1)2+(x-1)2)=(x-1)*sqrt(2) then f23\[\propto\]Q2*Q3/[(x-1)*sqrt(2)]
Since we want the equilibrium we have to pose |f12|=|f23| we already find the quadrant. Thus:
Q1*Q2/2=Q2*Q3/[(x-1)2*2]
since |Q1|=|Q2|=Q and |Q3|=4*Q
Q2/2=4*Q2/[(-x-1)2*2]
solving with respect to x (we need only the positive solution) we obtain x=1 and since y=x then y=1
First of all the add charge Q3 must stay on the line where Q1 and Q2 are placed, otherwise a non compesated force will be created. We can note that, in this case, the line connecting Q1 and Q2 is y=x.
If we place the charge on the first quadrant, then Q2 will be repulsed by Q1 and attracted by Q3 then the two forces will be directed on the same way so their sum will not be zero. If instead we place the charge on the third quadrant, Q2 will be replused by Q1 and attracted by Q3 with the two forces directed in opposite direction. Then this is our case.

In order to calculate the position we have to know that the force between two charges "Qa" and "Qb" place at a distance "dab" is proportional to:
f\[\propto\]Qa*Qb/dab2
the distance between Q1 and Q2 is d12=sqrt((0-1)2+(0-1)2)=sqrt(2) then f12\[\propto\]Q1*Q2/sqrt(2)
now the distance Q2 and Q3 is d23=sqrt((x-1)2+(x-1)2)=(x-1)*sqrt(2) then f23\[\propto\]Q2*Q3/[(x-1)*sqrt(2)]
Since we want the equilibrium we have to pose |f12|=|f23| we already find the quadrant. Thus:
Q1*Q2/2=Q2*Q3/[(x-1)2*2]
since |Q1|=|Q2|=Q and |Q3|=4*Q
Q2/2=4*Q2/[(-x-1)2*2]
solving with respect to x (we need only the positive solution) we obtain x=1 and since y=x then y=1
Last edited:
kakar133
Member level 2

it means that both Q2 and Q3 are at the same position.
OK, we are speaking here of instable equilibrium, that means the sum of forces on Q2 will be zero statically in the first time instant then the system will evolve.
First of all the add charge Q3 must stay on the line where Q1 and Q2 are placed, otherwise a non compesated force will be created. We can note that, in this case, the line connecting Q1 and Q2 is y=x.
If we place the charge on the first quadrant, then Q2 will be repulsed by Q1 and attracted by Q3 then the two forces will be directed on the same way so their sum will not be zero. If instead we place the charge on the third quadrant, Q2 will be replused by Q1 and attracted by Q3 with the two forces directed in opposite direction. Then this is our case.
In order to calculate the position we have to know that the force between two charges "Qa" and "Qb" place at a distance "dab" is proportional to:
f\[\propto\]Qa*Qb/dab2
the distance between Q1 and Q2 is d12=sqrt((0-1)2+(0-1)2)=sqrt(2) then f12\[\propto\]Q1*Q2/sqrt(2)
now the distance Q2 and Q3 is d23=sqrt((x-1)2+(x-1)2)=(x-1)*sqrt(2) then f23\[\propto\]Q2*Q3/[(x-1)*sqrt(2)]
Since we want the equilibrium we have to pose |f12|=|f23| we already find the quadrant. Thus:
Q1*Q2/2=Q2*Q3/[(x-1)2*2]
since |Q1|=|Q2|=Q and |Q3|=4*Q
Q2/2=4*Q2/[(-x-1)2*2]
solving with respect to x (we need only the positive solution) we obtain x=1 and since y=x then y=1
kakar133
Member level 2
Q2/2=4*Q2/[(-x-1)2*2] ?
how you obtained this step from the previous one , I mean (-x-1)^2. In the previous step it was (x-1)^2.
how you obtained this step from the previous one , I mean (-x-1)^2. In the previous step it was (x-1)^2.
No, because I used -x, then Q3(-1,-1). Don't forget we know the charge have to stay in the third quadrant.
albbg
Advanced Member level 4
You are right.
At first I used "x" as position for Q3, and I sent the post. After it seemed to me more understsadable to use "-x" so I corrected the equation. But I corrected only the last one, forgetting to update all the equations I wrote.
At first I used "x" as position for Q3, and I sent the post. After it seemed to me more understsadable to use "-x" so I corrected the equation. But I corrected only the last one, forgetting to update all the equations I wrote.
kakar133
Member level 2
Thank you very much.
You are right.
At first I used "x" as position for Q3, and I sent the post. After it seemed to me more understsadable to use "-x" so I corrected the equation. But I corrected only the last one, forgetting to update all the equations I wrote.
- Status
- Not open for further replies.
Similar threads
-
-
-
Kindly, I need this eBook urgently please "Handbook of Geostationary Orbits" by E.M. Soop. Thanks
- Started by Josephv
- Replies: 4
-
-
Help me to find the time constant of this circuit.
- Started by sel010913
- Replies: 8
