LC Circuit with variable filter?

[Jimmylee]

Hi, folks
The tank circuit below is designed according to LC Circuits Design Basics to have a variable resonance.

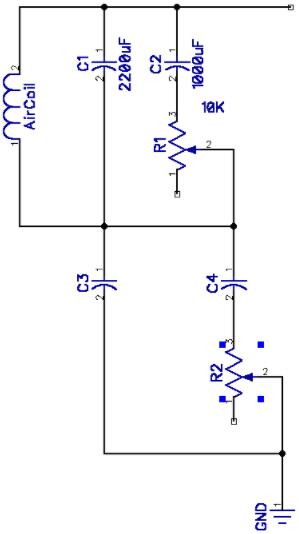
Can someone please tell me, in general terms, what the function of the lower two caps and pot would be? In other words, how they, and their selected values, affect the output of the entire circuit.

Anyone has ideas of it? Thank you in advance.

 

[danadakk]

The coil and C1 are the root parallel resonant circuit, so's to speak.

R1 and C2, change the resonance freq by effectively changing the reflected
C seen by the root root parallel resonant circuit. When pot set to 0 ohms
the resonance is determined by coil and sum of C1 and C2. As pot increases
in ohms less C2 reflected across tanks, so freq rises.

C3 forms a root series resonant circuit with coil. R2 C 4 do same f() as R1 C2 only
to the series resonant frequency.

So effectively you have a parallel resonant circuit in series with a a series resonant
circuit. The Z at terminal, depneding on values, would look somnething like this -

By C selection the peak and dip occurrence can be interchanged at the point
of freq they occur at.

Regards, Dana.

 

[betwixt]

Dana is correct but beware that the resistors in series with the capacitors, if not set to minimum value will introduce some strange impedance effects. Adding a variable resistor in series with a fixed capacitor does not make a variable capacitor!

Brian.

 

[danadakk]

Yes, series R with a C reflects an equivalent C in parallel with R. Thats a transform
often used in RF work. You can write the LaPlace equivalent of both networks,
set them equal to each other, to derive the effective C reflected.

Very useful in Z matching network work.

Equivalent impedance transforms - Wikipedia

en.wikipedia.org

This shows the transform equations -

**broken link removed**


Regards, Dana.

 

[Jimmylee]

Thank you for you all explanations.

As I understand, the upper tank circuit would (probably) be tuned to a specific frequency. The lower RC circuit then acts as a tunable high frequency cut-off for any such tuning.

Taking a specific example to clarify. Let's say the coil has an impedance of 10uH at 1120KHz, C1 and C2 are 1nF. R1 is 100K. That would provide a degree of "tuning" within the AM band.

Assuming R2 is also 100K, how would the values of C3 and C4 be calculated to perform the tunable high pass filter? In other words, to impose an entire tuning range of the upper tank circuit, what the parallel tank would do?

 

[FvM]

A tunable LC circuit needs variable L or C components. Although the characteristic of the circuit can be varied by means of R1 and R2, it's far from being a tunable LC filter. You would want to perform a simulation with variable resistor values to see why it doesn't serve as useful filter.

If you want to analyze the circuit in post #1 as filter, you should define in- and output nodes. The schematic doesn't have it.

 

[danadakk]

This is from the node point of view a tunable impedance. Freq can be tuned via R, as
confirmed by transform equations causing reflected C to change by changing R.

I will try to sim a R sweep in sim, no promises, to see if I can produce
results.

Alternatively use LaPlace and solve for Z from top of network to ground,
then use PFE to expand results to show R effect on |Z|. I would grind thru
it for you but have my own issues to solve.


Regards, Dana.

--- Updated Jul 21, 2021 ---

Playing around with circuit, for values show, its only at very low values
of pot R does one see shift in pole zero response. If the C i series with
pots much larger that unmodified C's there would be greater shift, but
again and relatively low values of pot R.

A varactor approach might be a better choice, eg post control varactor C.
But the bias network a tad complicated because of upper tank.


Regards, Dana.

--- Updated Jul 21, 2021 ---

Here is an example show zero shifted as R2 changes from 1 ohm to 100K ohm.

Regards, Dana.

--- Updated Jul 21, 2021 ---

Here is shift in pole as R 1 is changed from 1 ohm to 100 k.

Regards, Dana.

--- Updated Jul 21, 2021 ---

Pots by the way should be more like 100 ohms, as the feq shift
is very non linear with pot R and most of the shift occurs at low R.

Also note when shifting pole zero also moves significantly.


Regards, Dana.

 

[danadakk]

Here is a basic sim showing the reflected C change on resonance, R changed from 1 ohm to 100K.

Regards, Dana.

 

[dick_freebird]

"Load Pull" test rigs seem to like a sliding-core inductor
controlled by a servomotor.

The scheme of varying"effective L" by a series resistor
will make Q vary along with L. That may not deliver
the quality of inductor you want, at the more resistive
end of the tuning range.