gary36
Full Member level 4

Hi
I was just reading about convolution and I understood that input signal can be expressed as weighted sum of scaled and delayed impulse responses. In continuous domain, the definition is clear to me. But I am not clear about discrete domain definition.
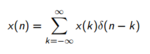
In a sampled system when we have fixed number of samples , how can k vary from -infinity to + infinity?
, how can k vary from -infinity to + infinity?
I was just reading about convolution and I understood that input signal can be expressed as weighted sum of scaled and delayed impulse responses. In continuous domain, the definition is clear to me. But I am not clear about discrete domain definition.
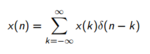
In a sampled system when we have fixed number of samples
Last edited by a moderator:

