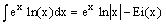subharpe
Full Member level 4

- Joined
- Jan 9, 2008
- Messages
- 207
- Helped
- 25
- Reputation
- 50
- Reaction score
- 2
- Trophy points
- 1,298
- Location
- Bangalore,India
- Activity points
- 2,657
Hi everybody, someone can give me the integration technique for the function
∫exp(x)*ln(x) dx? Somebody todl me it is not integrable. I want to know how is it non-integrable and if not, how to integrate it?
One way is to expand exp(x) and integrating. But I couldn't find a concrete result, the result comes in a series not in analytic expression.
∫exp(x)*ln(x) dx? Somebody todl me it is not integrable. I want to know how is it non-integrable and if not, how to integrate it?
One way is to expand exp(x) and integrating. But I couldn't find a concrete result, the result comes in a series not in analytic expression.