Integrating experimental data

[rakue]

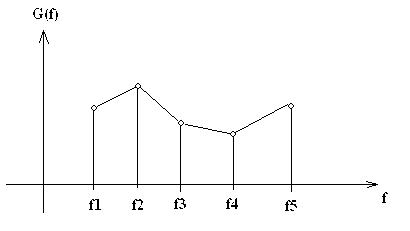
Hi, I don't know if this is the proper part of the forum to ask this, but I'm trying to figure out how I can obtain a certain value from an equation that contains an integral if I want to use experimental data. the equation looks like this:

B= (∫G(f)df)² / (∫G(f)²df)

where it is to be evaluated from 0 to ∞.

But to keep my question simple, say, my equation is: B= ∫G(f)df

Now, I have experimental values for "G(f)" and it's corresponding "f" (I'm not even sure if I'm understanding this correctly).

Is it right for me to simply, multiply the G's with their corresponding f's and then take the sum? So in effect, I'm basically doing this:

Ʃ(G_i*f_i) where i is the index for each value of f

Am I still integrating if I do this? If not, what should be the proper approach to this?

thank you very much for all your help!

 

[milind.a.kulkarni]

Hi

if it is the function B= ∫G(f)df in the continuous time then this will be represented by B = Ʃ(G[N]) where N is from 0 to Nmax ......So I thin what you are doing is Ʃ(Gi*fi) looks like different for B= ∫G(f)df

Good Luck

 

[albbg]

To approximate an integral there are many formulas. You approach is not correct because you have to consider "df" and not "f".
A simple method is to consider a trapezoidal integration.
Let's draw you points in a cartesian plane, then connect each pair of points with a line:

As you can see under the approximation of the curve there is a sequence of trapezi. The integral is the sum of all their areas. Since the area is given by (base1+base2)*heigh/2 then from the figure the i-th trapezium will have area:

Area(i) = [G(i+1)+G(i)]*[f(i+1)-f(i)]/2

the approximation of the integral, having datas over N points, will be given by:

\[Integral=\sum_{i = 1}^{N-1} Area(i)\]