Jarek Duda
Newbie

I have just prepared initial article: https://arxiv.org/pdf/2112.12557
Proposed numerically inexpensive model calculates electron diffusion based on entropy maximization ( https://en.wikipedia.org/wiki/Maximal_entropy_random_walk ), what gives stationary probability distribution exactly as quantum ground state – with Anderson localization e.g. preventing conductance in semiconductor, until exceeding some threshold voltage.
Works great for p-n junction, I will try to get further e.g. transistor.
Are there models like this in literature, software? If not, what real-life usage could it allow for? E.g. some technology optimization?
Ps. Such simpler simulator: https://demonstrations.wolfram.com/ElectronConductanceModelsUsingMaximalEntropyRandomWalks/
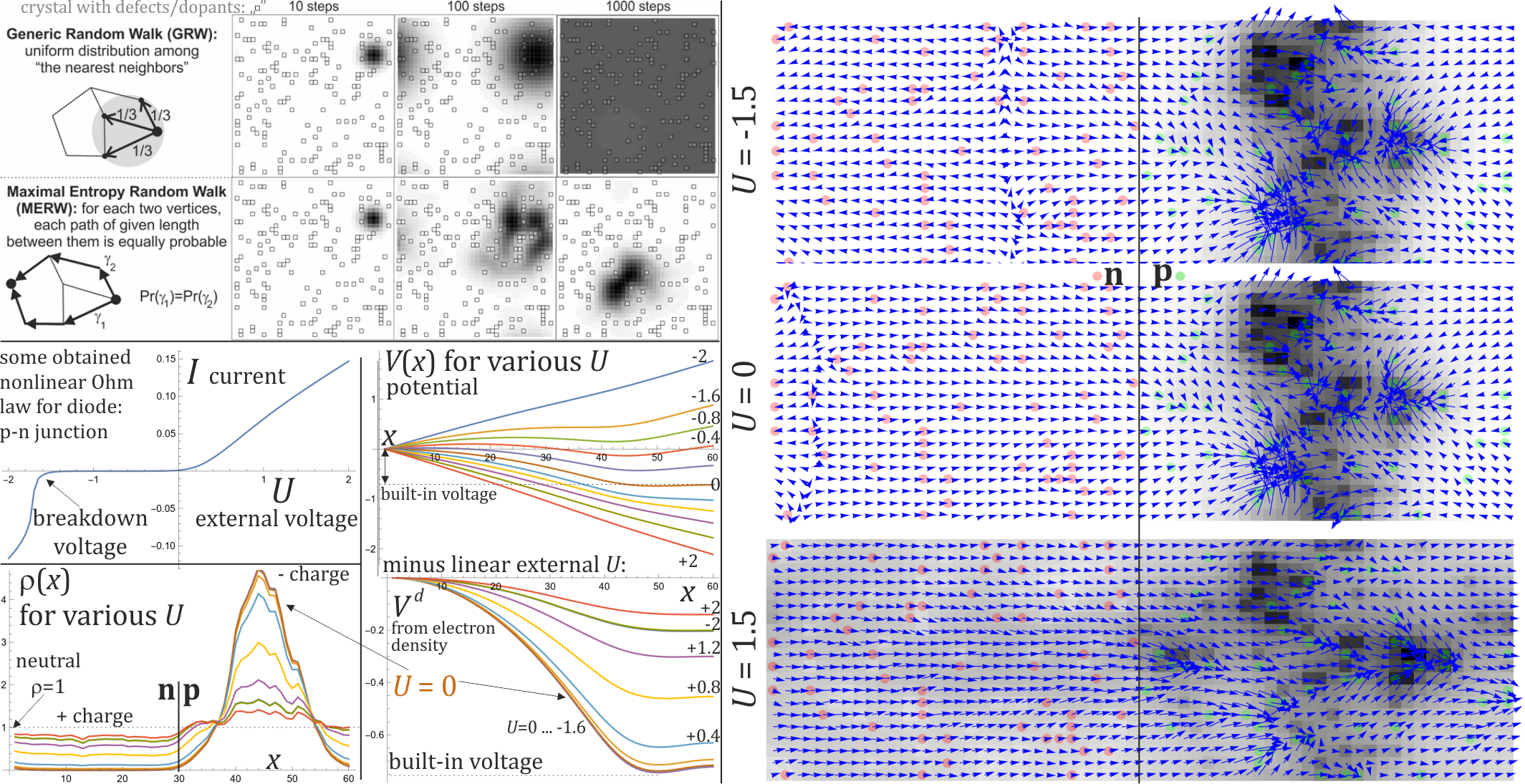
Brief model explanation: we assume electrons jump between neighboring atoms in semiconductor crystal, which has dopants - atoms of different type (fixed, randomly distributed), corresponding to specific potentials.
We choose V_{i,j} potential - energy associated with i->j transition between atoms, containing:
1) gradient from external voltage,
2) individual potentials of atoms, and
3) self-interaction potential from charge density (Poisson equation).
Without self-interaction (the hard part), we then just define transfer matrix:
M_{ij} = exp(-beta * V_{ij})
find its dominant eigenvector:
M psi = lambda psi
Getting MERW stochastic matrix of the diffusion defining currents:
S_{ij} = M_{ij}/lambda * psi_j / psi_i
Reddit discussion:
Proposed numerically inexpensive model calculates electron diffusion based on entropy maximization ( https://en.wikipedia.org/wiki/Maximal_entropy_random_walk ), what gives stationary probability distribution exactly as quantum ground state – with Anderson localization e.g. preventing conductance in semiconductor, until exceeding some threshold voltage.
Works great for p-n junction, I will try to get further e.g. transistor.
Are there models like this in literature, software? If not, what real-life usage could it allow for? E.g. some technology optimization?
Ps. Such simpler simulator: https://demonstrations.wolfram.com/ElectronConductanceModelsUsingMaximalEntropyRandomWalks/
--- Updated ---
Brief model explanation: we assume electrons jump between neighboring atoms in semiconductor crystal, which has dopants - atoms of different type (fixed, randomly distributed), corresponding to specific potentials.
We choose V_{i,j} potential - energy associated with i->j transition between atoms, containing:
1) gradient from external voltage,
2) individual potentials of atoms, and
3) self-interaction potential from charge density (Poisson equation).
Without self-interaction (the hard part), we then just define transfer matrix:
M_{ij} = exp(-beta * V_{ij})
find its dominant eigenvector:
M psi = lambda psi
Getting MERW stochastic matrix of the diffusion defining currents:
S_{ij} = M_{ij}/lambda * psi_j / psi_i
Reddit discussion:
Last edited:
