v9260019
Member level 2

Hello all
Given a curve C1, the evolute is the curve C2 defined by the loci of the centers of curvature of C1. In other words: construct in each point P of curve C1 a circle that is a tangent to C1 in P; then the center of the circle belongs to C2.
When C1 is given by (x, y) = (f(t), g(t)), then C2 has the form:
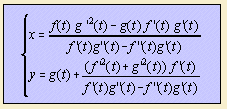
How to prove of the foumula above?????
Thanks a lot[/img]
Given a curve C1, the evolute is the curve C2 defined by the loci of the centers of curvature of C1. In other words: construct in each point P of curve C1 a circle that is a tangent to C1 in P; then the center of the circle belongs to C2.
When C1 is given by (x, y) = (f(t), g(t)), then C2 has the form:
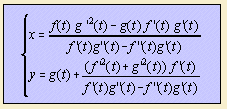
How to prove of the foumula above?????
Thanks a lot[/img]
