v9260019
Member level 2

Final value theorem
Hello all
the final value theorem is defined by
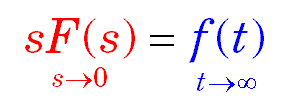
the final value theorem is valid only if F(S) has poles only in the left half-plane and ,at most ,one pole at the origin. If F(S) has poles in the right half-plane or poles on the imaginary axis other than at the origin , the final value theorem is invalid~~~~~ how to prove this and why
thanks a lot
Hello all
the final value theorem is defined by
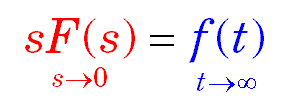
the final value theorem is valid only if F(S) has poles only in the left half-plane and ,at most ,one pole at the origin. If F(S) has poles in the right half-plane or poles on the imaginary axis other than at the origin , the final value theorem is invalid~~~~~ how to prove this and why
thanks a lot


