yefj
Advanced Member level 5

Hello, We express the radiation from a source by the expression bellow:
\[ U(x,y)=\frac{e^{jkz}e^{\frac{k}{2z}(x^2+y^2)}}{j\lambda z}\iint_{-\infty}^{+\infty}u(x',y')e^{-j\frac{2\pi}{\lambda z}(x'x+y'y)}dx'dy' \]
the fourier transform is \[f_x=\frac{x}{\lambda z}$ and $f_y=\frac{y}{\lambda z}\].\
Our system bellow has two apartures which has distance between them.
each aparture has fourier transform of sinc \[F(rect(ax)rect(by))=\frac{1}{|ab|}sinc(\frac{f_x}{a})sinc(\frac{f_y}{b})\]. \
\[F(\delta(f_x-\frac{a}{2},f_y-\frac{b}{2}))=e^{[i\pi(ax+by)]}\]. \
I know that convolution with delta is a shift in space.
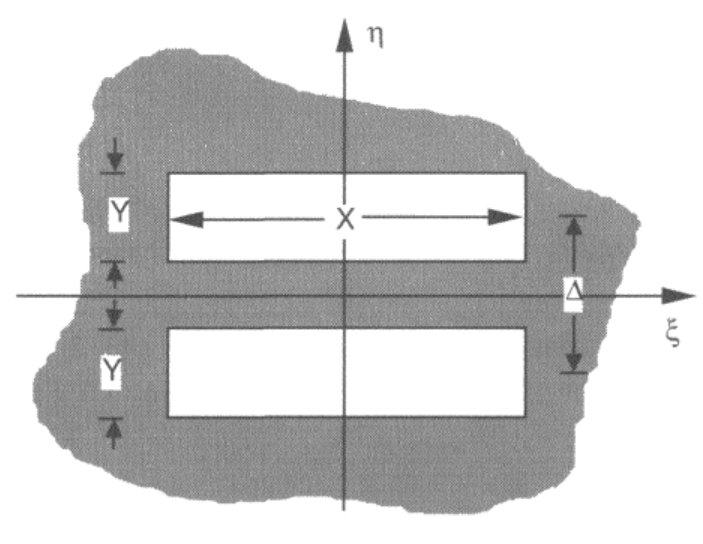
how to find using the integral expression shown above the fourier transform of the shape bellow?
Thanks.
\[ U(x,y)=\frac{e^{jkz}e^{\frac{k}{2z}(x^2+y^2)}}{j\lambda z}\iint_{-\infty}^{+\infty}u(x',y')e^{-j\frac{2\pi}{\lambda z}(x'x+y'y)}dx'dy' \]
the fourier transform is \[f_x=\frac{x}{\lambda z}$ and $f_y=\frac{y}{\lambda z}\].\
Our system bellow has two apartures which has distance between them.
each aparture has fourier transform of sinc \[F(rect(ax)rect(by))=\frac{1}{|ab|}sinc(\frac{f_x}{a})sinc(\frac{f_y}{b})\]. \
\[F(\delta(f_x-\frac{a}{2},f_y-\frac{b}{2}))=e^{[i\pi(ax+by)]}\]. \
I know that convolution with delta is a shift in space.
how to find using the integral expression shown above the fourier transform of the shape bellow?
Thanks.

