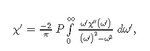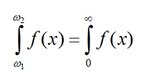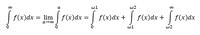m.mohamed
Member level 1

If I have a general integral equation with a semi-bounded limits from zero to infinity and I want to apply this equation on some deterministic values. The integration in this case must be converted to a deterministic integral, but how?
for example, in the equation below, I want to find the integral for a specific range of frequencies.
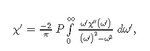
for example, in the equation below, I want to find the integral for a specific range of frequencies.