okami11408
Newbie level 4

I'm learning about the Fourier Series and have a few question.
First, we have 2 methods to find the Fourier coefficient of the Fourier Series.
1. Use the formula Cn below.
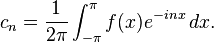
note that: x=2∏ft
2. Expand the function.
For Example I have y(t)=3cos(2∏9t)+4cos(2∏8t), let use the Expansion method
y(t)=3cos(2∏9t)+4cos(2∏8t) <---- Already expand
we have
y(j2∏9t)=3 at f=9 Hz Fourier coefficient=3/2
y(j2∏8t)=4 at f=8 Hz Fourier coefficient=4/2
Note:I devided by 2 for two side analysis.
This method makes sense to me.
but when it comes to use of formula Cn, it becomes nonsense.
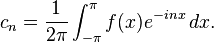
note that: x=2∏ft
My question is how come multiply the whole function with sine & cosine at some
particular frequency and integrate it. it turns into the Fourier coefficient.
I mean why is that actually work? It's an area, how can that related to the coefficient.
I want some intuition.
Thank you!
First, we have 2 methods to find the Fourier coefficient of the Fourier Series.
1. Use the formula Cn below.
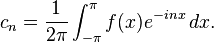
note that: x=2∏ft
2. Expand the function.
For Example I have y(t)=3cos(2∏9t)+4cos(2∏8t), let use the Expansion method
y(t)=3cos(2∏9t)+4cos(2∏8t) <---- Already expand
we have
y(j2∏9t)=3 at f=9 Hz Fourier coefficient=3/2
y(j2∏8t)=4 at f=8 Hz Fourier coefficient=4/2
Note:I devided by 2 for two side analysis.
This method makes sense to me.
but when it comes to use of formula Cn, it becomes nonsense.
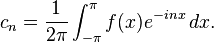
note that: x=2∏ft
My question is how come multiply the whole function with sine & cosine at some
particular frequency and integrate it. it turns into the Fourier coefficient.
I mean why is that actually work? It's an area, how can that related to the coefficient.
I want some intuition.
Thank you!
