yefj
Advanced Member level 5

Hello , i have a general model of a power delivery network from my DC connector to the IC port shown below.
then i added a load and put a 0 to 6 Volt pulse.As you can see below i get 280mV at most which means that the inductors and capacitors didnt charge enough.
Could i see what will happen in the time domain pulse from the frequency domain plot?
Thanks.
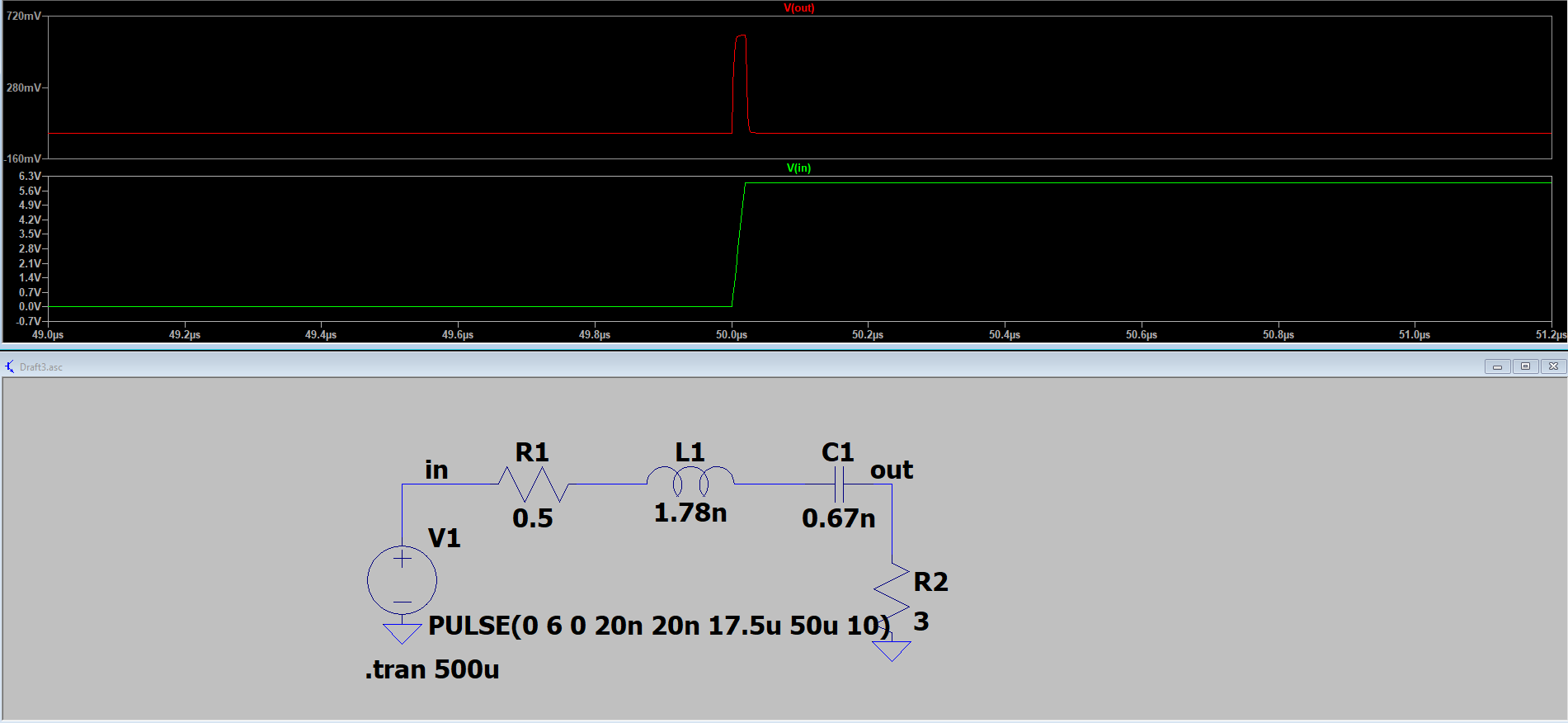
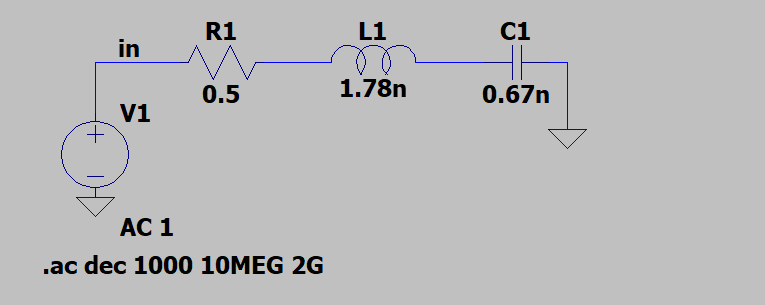
then i added a load and put a 0 to 6 Volt pulse.As you can see below i get 280mV at most which means that the inductors and capacitors didnt charge enough.
Could i see what will happen in the time domain pulse from the frequency domain plot?
Thanks.

