Finding the impedance and the quality factor in RLC circuit

[husny540]

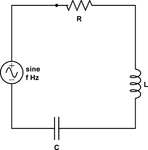
An RLC circuit is tuned to the frequency of 90.9MHz.Calculate the R,L,C values for this specification by mentioning the assumptions made(it is given that you cannot avoid having a resistance 12 ohm and inductance of 1.29 micro henri). Also calculate the total impedance and the quality factor of the circuit.

what i attempted:
resonant frequency equation is fs=1/2π√LC. as the sum says to calculate the R, and L i have considered 12 ohm as the resistance because the resistance is already given eventhough the R is said to be calculated and i have calculated inductance as 1.29 microhenri as it is already given. Now to find the capacitance, by substituiting the frequency and inductive values to the above equation i calculated the capacitance to be 2.37*10^ -15. Are these correct ? if so how can i find the total impedance and quality factor. Is the total impedance equation Z=√(R^2 )+√(〖X_T〗^2 ) and what about the quality factor. Please help

 

[barry]

I came out with a value of 2.38 x 10^-12 for the cap.

Impedance is calculated by: z=sqrt(R^2 +(XL-XC)^2); (XL=reactance of inductor, XC is reactance of capacitor)

Q is calculated by : Q=ws * L/R

 

[chuckey]

If its a series tuned circuit then the impedance at resonance = R, which are all the resistive losses rolled up into one because Xc = Xl, so Zl-XC = 0 .
Frank

 

[husny540]

Thankyou for helping me and i'm having a question related to this. Suppose the antenna input recieves a signal of V=20sin(omega*t+pi/6). Find an equation for the generated current. And how can i draw the phasor diagram for this and sketch the signals in a time domain graph ? Please guide me

- - - Updated - - -

Yes the capacitive value ends with 10^-12 not ^ -15.my mistake. Thank you for the correction

 

[chuckey]

Phasor diagram, its the current that flows through the circuit. So vertical line to represent the supply current. The voltage drop across the resistor is in phase with this so put an arrow on the current vector to represent the Volt drop across the resistor (equals the supply voltage). Remember CIVIL, so in a capacitor the current leads the voltage so on your phasor, the Vcap is lagging the current so line at 90 degrees to the left from base of current vector, scaled to the Vr vector. In an inductive circuit, I lags the voltage, so in your phasor, the VL lies opposite the Vc vector and is the same length.
Frank

 

[husny540]

Thankyou for the explanation but i didn't get a clear idea, can you help me with a diagram? can you answer this question which i posted you earlier-Suppose the antenna input recieves a signal of V=20sin(omega*t+pi/6). Find an equation for the generated current.

 

[KerimF]

The total impedance (Z) seen by the voltage source is:
Z = R + jwL + 1/jwC = R + j(wL-1/wC)
( j*j = -1 )

To apply I = V / Z, V(t) in the time domain should be converted first to the phasor domain as

V = Vp /_φ_ = 20 /_pi/6_

Could you find the value of Z, written as Z = R + jX?
I assumed that 'omega' of the given v(t) is for 90.9 MHz... right?
Oh sorry, in this case X=0 and Z = R only.

Perhaps we have to take Z as R + j(wL-1/wC) and get Z(w), Z in function of w.

By knowing Z(w) as R + jX(w), we can find Z as |Z| /_φ_ (the polar phasor of Z) also in function of w. Do you recall how?


Note:
If V = |V| /_φv_ and Z = |Z| /_φz_ , the current is:
I = |I| /_φi_
where:
|I| = |V| / |Z|
φi = φv - φz

The phasor I could be converted then to the time domain as I(t)... we will see how

 

[chuckey]

"l of V=20sin(omega*t+pi/6)." This is a sine wave of peak amplitude 20 volts. The frequency is given as (omega*t+pi/6)/2 PI. So until we can put some numbers into the frequency equation, we don't know the frequency. On the other hand if it equals 90.9 MHZ (the resonant frequency) then the current is 20 X .707/12 amps. I'll try and send a phasor diagram on a second posting.
Frank

- - - Updated - - -