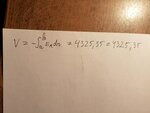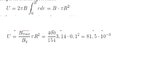Salvador12
Full Member level 4

Hi folks, so my problme is I've been given the formula actually more than 1 version of the formula but I can't seem to solve it because my maths are very bad.
Can you please provide me a formula for calculating the voltage from a Faraday disc? I would also be happy if someone could show the calculation process using the parameters that I will give here so that I see how they insert into the various parts of the formula?
B field strength 1 Tesla, rotation = 1000 rpm/min , disc radius 15cm.
I seem to have problems because the voltage in each next segment of the disc is different due to larger radius having higher angular velocity and I can't incorporate this into the equation.
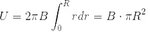
Can you please provide me a formula for calculating the voltage from a Faraday disc? I would also be happy if someone could show the calculation process using the parameters that I will give here so that I see how they insert into the various parts of the formula?
B field strength 1 Tesla, rotation = 1000 rpm/min , disc radius 15cm.
I seem to have problems because the voltage in each next segment of the disc is different due to larger radius having higher angular velocity and I can't incorporate this into the equation.