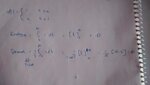example of power and energy signal

[Bhuvanesh123]

1)All periodic signal are power signal but all power need not to be periodic signal . We have familiar example step signal.but i cant agree with that see my below derivation(attached file) and correct me

2)all non periodic signal are energy signals but vice versa is not true. could you give me an example for this .

 

[zorro]

1) Your attachment is wrong:
You must take the limit for T->Inf with the upper limit of the integral = T instead of Inf .
On the other hand, Inf/Inf is not Inf .

2) "all non periodic signal are energy signals" is wrong. Surely you can find many examples by yourself.

Z

 

[yavuzyaman]

What do you mean by saying "power signal" and "energy signal" ? You can find the energy or power of every periodic/aperiodic signals. Energy or power is a constant value.
On the other hand, yes unit step or delta functions has theoretically infinite energy and power. But keep in mind that practically they are not applicable. They are defined for only convenience on notation.

-yavuz

 

[doraemon]

Hello!

On the other hand, yes unit step or delta functions has theoretically infinite energy and power. But keep in mind that practically they are not applicable. They are defined for only convenience on notation.

I'm not sure whether we talk of the same delta but the Dirac distribution has by definition an energy of one, therefore finite.

The step function has a finite power.

Dora.

 

[zorro]

There is some confusion around.

What do you mean by saying "power signal" and "energy signal" ?

"energy signal" : signal of finite energy
"power signal" : signal of infinite energy but finite power

... but the Dirac distribution has by definition an energy of one, therefore finite.

Dirac distribution has by definition an "area" of one, but its energy is infinite.

In all the above, energy and power are defined via intergrals between -Inf and Inf.

Regards

Z

 

[yavuzyaman]

Hi,

Doraemon is right! Dirac delta function (or distribution) has finite energy of 1. My bad, sorry my wrong sentence.
What I tried to write is unit step has infinite energy. But finite power of 1/2. Dirac delta function has finite energy but has infinite power.

But when I search for it, I realized that I am still wrong for dirac delta. It has finite energy yes, but it has also finite power of zero.

Thanks doraemon and zorro

 

[bilal_oct]

Please have a look the attached slides for energy and power signals

 

[Bhuvanesh123]

You must take the limit for T->Inf with the upper limit of the integral = T instead of Inf .

why t instead of infinity we calculate power for infinite period, is it not?

 

[FvM]

The correct power value for the step function is 1. You can achieve it either by integrating over a finite period of your choice (T doesn't matter because the signal is constant) or an infinite period.

 

[zorro]

... Dirac delta function (or distribution) has finite energy of 1.
...
... I realized that I am still wrong for dirac delta. It has finite energy yes, but it has also finite power of zero.

Please don't confuse area (integral of f(t)) with energy (integral of |f(t)|^2).

One of the ways to represent a delta is taking a pulse of unit area and make its duration shorter and shorter.
Please consider a pulse of duration "a" and height 1/a, such that its area is unity.
Its energy is 1/a . Right?
Now, as "a" approaches 0, that pulse "resembles" more and more a Dirac delta. Its area is always 1, but its energy 1/a goes to infinity.

It doesn't make sense to calculate the power of the delta: it wuold be a limit for a->0 and T->Infinity.
If you try to calculate the double limit, it doesn't exis because the result is dependent of the way the limit is reached.

why t instead of infinity we calculate power for infinite period, is it not?

We must put T as the upper limt of the integral and then T->Infinity.

Z