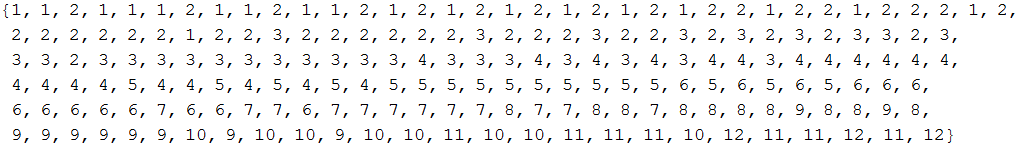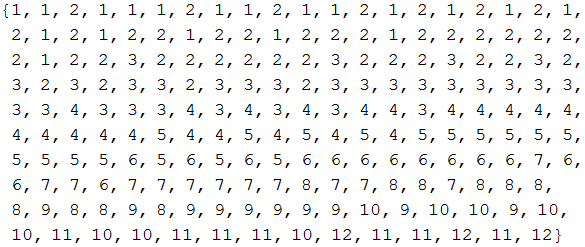E192 series formula (and formula for other series as well)

[uoficowboy]

I'm working on a Excel calculator and have run into something odd. My understanding was that you could calculate standard resistor values via this formula:

100*ROUND(10^(X/Y),2)

where Y is the series (E48, E96, E192), and X is any number from 0 to 47/95/191. I also thought that you could do the same for the E6/E12/E24 ranges, except with the rounding to 1 decimal place instead of 2.

However, this formula only seems to work for E48 and E96 and 191/192 E192 values. Specifically - 10^(185/192) = 9.19479. So rounding to two decimal points gives you 9.19. But In every E192 table I see I see this listed as 920. What's the deal here?

Also - the above formula misses all over the place for the E6/E12/E24 ranges - it produces values like 320 instead of 330, 460 instead of 470, etc.

Any help with making a better formula?

Thank you!

 

[andre_luis]

However, this formula only seems to work for E48 and E96 and 191/192 E192 values. Specifically - 10^(185/192) = 9.19479. So rounding to two decimal points gives you 9.19. But In every E192 table I see I see this listed as 920. What's the deal here?

The E192 series provide a tolerance of 0,5%, which for the 920Ω resistor would give 4,6Ω, but considering that the ratio of linear values in a division gives a logaritmic scale, the rounding rule is not exactly in the half of two consecutive numbers, but few below, so there is no issue to round the calculated value 919,47 to 920. Keep in mind that the aim of these series is to provide an equaly spaced resistance series not in a linear scale, but in such a way that some value divided by the immediatelly lower value is constant number for the whole table.

 

[FvM]

I presume there's no formula. The resistor values have been arbitrarily defined by a standard comitee, that's it. Use the published resistor series values in your spread sheet.

 

[The Electrician]

A logarithmic formula was used for the E48, E96 and E192 series. See here for details: https://forum.allaboutcircuits.com/threads/why-do-electronic-components-have-such-odd-values.138056/

 

[FvM]

As stated in post #1, E192 has an exception from the ideal geometric series 10^(1/192), E48 and E96 are exact. Classical E6 - E24 are roughly geometric, but there's no applicable formula.

 

[c_mitra]

Honestly I do not know but I guess it is a genetic error that has propagated for so long that little can be done now. Only thing we can safely do is to speculate!

 

[FvM]

Honestly I do not know but I guess it is a genetic error that has propagated for so long that little can be done now. Only thing we can safely do is to speculate!

I don't know the original source, but the Wikipedia explanation (in the German article) that it's an intentional rounding to achieve a more uniform series sounds very plausible.

 

[The Electrician]

I don't know the original source, but the Wikipedia explanation (in the German article) that it's an intentional rounding to achieve a more uniform series sounds very plausible.

What are you talking about here? Is it the apparent discrepancy at 9.20 in the E192 series? If so, how does that single point lead to a more uniform series?

 

[FvM]

Sure it does, the E192 series is 9.09, 9.20, 9.31, better than individually rounded 9.09. 9.19, 9.31

- - - Updated - - -

The empirical rounding rule applied in this case is that the increment shouldn't vary more than 1 digit between adjacent steps.

 

[andre_luis]

Each series "E-n" is considered as the logarithmically equidistant distribution of "n" values within the whole scale from 1 to 10. Perhaps a more convenient approach would be to plot a continuous curve with the expected value, and see if that specific value of the E-series standard is closer to which other neighbor value of the expected curve - on a log scale - to make a visual check to see if the rounding makes sense on that scale.

 

[FvM]

I must confess, I've limited motivation to harp on about the single E192 series value 9.20.

The applied rounding is obviously implementing a local (differential) rather than global (integral) uniformity rule. Although the chosen value has a larger distance to expected value 9.1948, it lays nearer to the geometrical center of preceding 9.09 and succeeding 9.31.

 

[andre_luis]

Considering that the OP already has the formula already implemented in Excel, with little extra effort could use the plotting capabilities of that tool to do that. Although I gree with you that we could find some sense here and there, there could have also inconsistencies aswell, and in general a visual inspection in the whole data set give a more comprehensive view of the amount of exceptions, if there are.

 

[c_mitra]

A possible explanation, (it is not accurate in mathematics) is that you take the first value (1 in this case), multiply by the geometrical progression factor (10^(1/192)=1.012064831) to get the next number, round it off and repeat. AND this will be simpler in your excel!!

Perhaps you will get better agreement.

- - - Updated - - -

I always thought that the 1-2-5 sequence we see on many instruments is THE E3 SERIES.
(and I am still learning)

 

[The Electrician]

Sure it does, the E192 series is 9.09, 9.20, 9.31, better than individually rounded 9.09. 9.19, 9.31

- - - Updated - - -

The empirical rounding rule applied in this case is that the increment shouldn't vary more than 1 digit between adjacent steps.

Then what is the empirical rounding rule in the E48 series? The increment in that series is sometimes 1, sometimes 2 and one time it's 3. What rule is that?

No such rounding rule was used in the making of the E192 series. The standard clearly describes the formula. The values are a geometric series with values geometrically spaced from 1 to 10, and 3 significant digits determined by multiplying the formula value by 100, rounding to the nearest integer and then dividing by 100. The 3 series E48, E96 and E192 encompass 336 values These values were calculated in the 1940s without modern electronic calculators--a rounding error was made in one of them.

I explain in the linked thread above the reasons for the strange values in the E6, E12 and E24 series that don't seem to fit a logarithmic formula. They started out with a logarithmic series and adjusted it for reasons of economy.

 

[FvM]

These values were calculated in the 1940s without modern electronic calculators--a rounding error was made in one of them.

Might be, believe it or not. I see no harm in turning to this or the other explanation.

No open questions, I think.

 

[The Electrician]

Each series "E-n" is considered as the logarithmically equidistant distribution of "n" values within the whole scale from 1 to 10. Perhaps a more convenient approach would be to plot a continuous curve with the expected value, and see if that specific value of the E-series standard is closer to which other neighbor value of the expected curve - on a log scale - to make a visual check to see if the rounding makes sense on that scale.

I don't think such an approach would be more convenient than just using the known formula for a geometric series. When calculating the E192 series just test for the value 9.19 and replace it with 9.20--problem solved. For the E48 and E96 series, the known formula gives the correct result for the entire series.

- - - Updated - - -

Believe it or not.

What's your answer to the question I asked you: Then what is the empirical rounding rule in the E48 series? The increment in that series is sometimes 1, sometimes 2 and one time it's 3. What rule is that?

- - - Updated - - -

The applied rounding is obviously implementing a local (differential) rather than global (integral) uniformity rule. Although the chosen value has a larger distance to expected value 9.1948, it lays nearer to the geometrical center of preceding 9.09 and succeeding 9.31.

What about the value 1.64 in the E192 series? The values in the actual E192 series on either side are 1.62 and 1.65. The geometric mean of those two is 1.63493 which would round to 1.63, but the exact value determined from the formula is 1.63509 which rounds to 1.64. The geometric mean does not give the value which is actually in the E192 series.

 

[FvM]

What's your answer to the question I asked you: Then what is the empirical rounding rule in the E48 series? The increment in that series is sometimes 1, sometimes 2 and one time it's 3. What rule is that?

A possible rule: Rounded geometric series + the inclement has to be monotonous. 9.19 would be the only violation.

 

[The Electrician]

A possible rule: Rounded geometric series + the inclement has to be monotonous. 9.19 would be the only violation.

I'm sure you mean monotonic rather than monotonous--a totally different word in English.

The increments are not monotonic in E48. Here are the increments:

Here are the changes in the increments in the E48 series:

- - - Updated - - -

The increments in the E192 series are not monotonic either. Herewith a list of the increments:

And the first differences in the increments:

- - - Updated - - -

Might be, believe it or not. I see no harm in turning to this or the other explanation.

No open questions, I think.

What if those other explanations don't work for the whole series? Some people want to know the actual method the people who did these calculations in the 1940s used.

- - - Updated - - -

A possible explanation, (it is not accurate in mathematics) is that you take the first value (1 in this case), multiply by the geometrical progression factor (10^(1/192)=1.012064831) to get the next number, round it off and repeat. AND this will be simpler in your excel!!

Perhaps you will get better agreement.

- - - Updated - - -

I always thought that the 1-2-5 sequence we see on many instruments is THE E3 SERIES.
(and I am still learning)

If you multiply the progression factor by the previous value BEFORE it was rounded, then you will get the exact values in the E48 and E96 series, and also the E192 series except for the one value 9.20 under discussion.

 

[andre_luis]

When calculating the E192 series just test for the value 9.19 and replace it with 9.20--problem solved

I can't see any general rule on that at all, as mentioned above, the decision to round based only on an assumption does not explain whether there is a mathematical reason or not. Until an overall analysis is done on the correct (logarithmic) scale, we will be in an endless debate.

 

[The Electrician]

For the person who just wants a formula that will give the values in the actual E192 series, including the 9.20 value, making a small change to the value 192 used in the formula will do the job.

The formula accepts as input the value n, which is the nth resistor value (starting with zero) in the E192 series, divides it by 192 and raises 10 to that power. If the value 192 is changed to 191.9977 this will return all the correct values in the E192 series.

Here are the values returned by this formula:

- - - Updated - - -

In post #18, I grabbed the wrong table for the increments in E48. The one shown is a duplicate of the E192 increments.

Here is the correct table of increments for E48:

- - - Updated - - -

I can't see any general rule on that at all, as mentioned above, the decision to round based only on an assumption does not explain whether there is a mathematical reason or not. Until an overall analysis is done on the correct (logarithmic) scale, we will be in an endless debate.

It's not a general rule. It is a fix for the incorrectly rounded value 9.20 in the E192 series. It is an answer for the OP who wants to have a program to calculate the values for the various resistor series. No analysis of anything is needed. The actual values of the E192 resistor values used in commerce are the ones from the known logarithmic formula with the exception of the 9.20 value, and that exception is due to a rounding error made in the 1940s, which was unnoticed for so long that it is now fixed in stone. A person who wants a program to generate actual, as used in commerce, E192 values can use the logarithmic formula, test for the value 9.19 and change it to 9.20.