asrock70
Full Member level 4

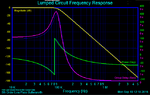
Is Mathematical dependence between quality of generated sinus , for example THD and number of point generated with DAC in DDS?
Alternatively between DAC resolution and THD ?
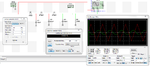
For example DDS AD9833 have 10bit DAC and 25MSPS , for sinus on 100kHz generate 250point in period
DAC in STM32F303 have 1MSPS and 12bit DAC for sinus 100kHz generate 10 point on period
how quantify qualitative difference between sin generated from AD9833 and STM32F3?
Alternatively between DAC resolution and THD ?
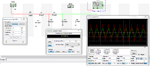
For example DDS AD9833 have 10bit DAC and 25MSPS , for sinus on 100kHz generate 250point in period
DAC in STM32F303 have 1MSPS and 12bit DAC for sinus 100kHz generate 10 point on period
how quantify qualitative difference between sin generated from AD9833 and STM32F3?