Create RMS averaged power spectrum based on complex data from FFT

[alex_wouter]

Hello,

I would like to create a RMS averaged power spectrum based on complex data from FFT.

In my project, i record 16384 samples at 25 Mhz sampling frequency and I cut the record in 8 parts. I apply 8 differents FFT from this record, so 2048 samples by FFT.

I convert all received datas into magnitude [sqr(Im²+Re²)], and after into dB.

So I have 8 spectrums of decibel magnitudes.


To create the RMS spectrum, should I need to convert magnitude into RMS values or temporal values into RMS before do the average ?


Do you think i need to use the following equation for each frequency with N = 8 and |xn| as magnitude.

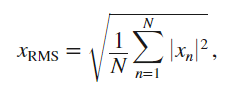
I based my reflexion from this article : https://www.dsprelated.com/showarticle/1159.php

Thanks for your help,

Alex

 

[andre_luis]

I apply 8 differents FFT from this record

It is not clear whether you mean you'll use shifted values of 8 interleaved samples, or calculate the FFT at 8 different times? By the way, the cited article refers to a method of dynamically change the rate of increasing weights to more recent moving average samples, something not considered in the above formula. In order to meet their approach, you should explicitly split the "Sum" symbol into 8 additions and then apply multiply factors to each one, having a greater weight the more recent the analysis.

 

[alex_wouter]

Thanks for your repply Andre.

I apply the same FFT for the 8 parts of the temporal signal, so 8 FFTs at differents times. I store all 16384 datas and treat them in the order (2048 by 2048) to obtain 8 spectrums of decibel magnitudes.

To be more precise, I would like to do the same compute that is done with the FFT Spectrum VI from National Instruments - FFT Spectrum (Mag-Phase) for 1 Chan.

Product Documentation - NI

zone.ni.com

The VI is configured with the RMS Average and exponential averaging mode.

You suggered to apply a formula like this for each frequency step to create the RMS average power spectrum ?

In this case, the more recent datas have a higher weight.

Alex

 

[KlausST]

Hi,

If Im not mistaken:
Adding RMS values with square/square root applies only for independent frequencies.
For identical frequencies you need to (add all real parts) and (add all imaginary parts) without squaring.
Then calculate the RMS from these real and imaginary values.

To check:
Add the squared RMS vaues of all frequencies after calculation (= Power of all frequencies)
it should be the same as the add of squares of the values before FFT (time domain). (= power of all v(t))
(FFT must not modify total power)

The RMS calculation of post#3 is a filtered RMS calculation, it will give correct
(BTW: I see two times X8 but miss X1. I guess this is a mistake)

Klaus

 

[alex_wouter]

Hi Klaus,

I think it is a filtered RMS calculation that is done in NI FFT Spectrum.

So the calculation in post#1 can't be applied in the case of RMS Exponential Averaging ?

From the article by dsprelated ( post#1), it is written : "If you take the square root of the average of the squares of your sample spectra, you are doing RMS Averaging." It is about compute a unique value from all frequency of one spectrum and no averaging many spectra together ?


How to calculated RMS from a couple of a real and imaginary values ?


Sorry, it was a mistake for the formula of post#3.

This formula can not be used if I should add imaginary and real parts separately.


Thanks for your help,

Alex

 

[KlausST]

How to calculated RMS from a couple of a real and imaginary values ?

The result of the FFT is for each frequency: The real part and the imaginary part.

Each pair forms a vector. And the length of the vector is the RMS value (if I´m not mistaken)
The length of the vector is: sqrt(imag^2 + real^2).

With tangens you may calculate the phase shift.

For more reliable informations read FFT docu.

Klaus

 

[alex_wouter]

I did not realize that when I was compute magnitudes, it was already RMS values that I obtain.

That was the first question of post#1, thank you.

Alex

 

[KlausST]

Hi,

again, just to be sure I´m not misunderstood:
for same frequency: you need to calculate the sum of all imags and the sum of all reals.
(= add all vectors)
After that you calculate the RMS. (length)

Klaus

 

[andre_luis]

The sum of all multiply factors should give 1/N ( = 1/8 = 0.125 ) whereas the above set give 0.96 ( = 0,19+0.14+0.12+0.11+0.8+0.7 )

 

[alex_wouter]

Klaus,

If I compute the sum of all imaginary and the sum of all reals and after computes the length, should I multiply each vector with the associated coefficient to do the exponential averaging ?

coeff1(Xa1+iXb1) + coeff2(Xa2+iXb2) + ... + coeff8(Xa8+iXb8) ?

___________________________

Andre,

To make the exponential Averaging I need to use the following formula :

With Yn(f) is the average value, Yn-1(f) is the old average and Xn is the value on the spectrum

When I decompose the equation with N = 8, I obtain around 0.65 as result of the multiply factors sum. I multiply the factors by around 1.52 to normalise the sum to obtain 1. Should I normalize to obtain 1/N ?

Thanks,

Alex

 

[andre_luis]

To make the exponential Averaging I need to use the following formula

It is perhaps considering after a big number of additions would become more and more close to 1 ( = 0.99... ).

Should I normalize to obtain 1/N ?

There is no impediment for that.