calenosa
Newbie level 5

From a Control Theory book I have:
"The frequency response function describes the steady-state response of a system to sinusoidal inputs. For a linear system, a sinusoidal input of a specific frequency results in an output that is also a sinusoid with the same frequency, but with a different amplitude and phase. The frequency-response function describes the amplitude change and phase shift as a function of frequency."
The above quotation is true, however, it doesn't say anything about the dc component in the steady-state response.
When I simulated the following system in MATLAB/Simulink:
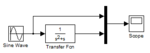
The source is a pure sine wave generator with no bias. I got the following response:
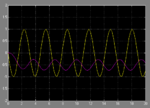
It can be seen that the response has a dc component, and I believe that the simulation result is correct. Therefore my question is can I calculate the dc component from the frequency response approach? If the answer is Yes, how can I do that?
Thank you.
"The frequency response function describes the steady-state response of a system to sinusoidal inputs. For a linear system, a sinusoidal input of a specific frequency results in an output that is also a sinusoid with the same frequency, but with a different amplitude and phase. The frequency-response function describes the amplitude change and phase shift as a function of frequency."
The above quotation is true, however, it doesn't say anything about the dc component in the steady-state response.
When I simulated the following system in MATLAB/Simulink:

The source is a pure sine wave generator with no bias. I got the following response:

It can be seen that the response has a dc component, and I believe that the simulation result is correct. Therefore my question is can I calculate the dc component from the frequency response approach? If the answer is Yes, how can I do that?
Thank you.


