Confusing with "States" of a System

[yemi11]

Let say we have pendulum system.



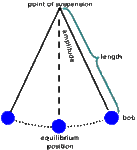
Which could be represented by a second order differential equaiton.
Solution comes with two integration constant and needs initial conditions...

Now, we are saying that, system have two states, and with these states, we can solve the system at any moment uniquely!

The states are, current angle and angular velocity.

If we don't know current angle, which easyly understandable, solution will be meaningless.
If we don't know angular velocity, we know the current angle but we don't know which way pendulum swinging.

Everything looks clear but i don't understand why we don't need to know about, let say, angular acceleration?
Okay i know, it looks clearly we don't need it by looking differential equation, even there is no term occures for its initial condition.

I wonder much more physical explanation.
Let say, we now the angle of a ball and angular velocity (we know two states),
what about if system has a very much acceleration in that moment even that cause system swing opposite side?

Yes. This is my question.

 

[andre_luis]

Everything looks clear but i don't understand why we don't need to know about, let say, angular acceleration?

If a particular condition is not observable by one of that 2 state variables, then this information must be obtained indirectly, since the whole system behavior is described as a well-defined equation. If I remember correctly, for the specific case to take this information ( instantaneous angular acceleration ), you should perform another differentiation in the time domain of the angular velocity, which is already one of the explicit variables, as you has defined.

 

[_Eduardo_]

.......
Let say, we now the angle of a ball and angular velocity (we know two states),
what about if system has a very much acceleration in that moment even that cause system swing opposite side?
.......

You cannot use the approximation for small angles (which leads to a 2nd order differential equation with constant coefficients), the solution of this equation is an elliptic integral.

https://en.wikipedia.org/wiki/Pendulum_(mathematics)#Arbitrary-amplitude_period

 

[andre_luis]

well-minded.
I would just add a remark:

You cannot use the approximation, unless for small angles

 

[_Eduardo_]

Thanks Andre.