Characteristic function of the system

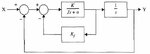
Hey, guys.

I'm studying the Automatic Control Systems and struggling with characteristic fn.

I'm given a system diagram as an attachment and I got my answer, but it's different from the solution.

My answer is

Transfer function : K/(JS^2 + aS + K*Kf*s +K)

But the answer from the solution is

Transfer function : (K*Kf) / [JS^2 + (aS + K*Kf)s +K*Kf]

As you noticed, there're Kf added on each.

Am I wrong or is solution wrong. I've been struggling with this for 3 hours and can't see

any problem from mine.

(The way I solved this is, I considered the system as two separate closed-loop. Firstly, calculated the first closed-loop in the middle then multiplied by 1/s. Then calculated as a closed-loop again with it. )

And another question is, I need to draw Nyquist plot with transfer function above. Normally the transfer function is given as a form of 'G(s)/[1 + G(s)H(s)], so I can draw the Nyquist plot with open-loop function G(s)H(s).
But with the function above, I can't seem to seperate G(s)H(s). How can I do this?

Could somebody help me with this matter?
Thanks a lot for your time.

Hi glorimda,

1.) The first transfer function (your answer) is correct. That means: The second one is false.

2.) You want to find the Nyquist plot "with transfer function above"? I don`t think so. What you really want (according to your expression G*H) is the Nyquist plot for the LOOP GAIN, correct?
In your case, you have nothing to do than to multiply the transfer function of the local (inner) block with feedback by 1/s. That is the gain of the open (major, outer) loop.
That means: Loop gain LG=K/[s(KKf+a)+Js^2]

Good luck
LvW

- - - Updated - - -

Remark: The characteristic function of the system is identical to the denominator of the transfer function, that means: 1+Loop gain=1+LG

Thanks, LvW. I wanted somebody to check whether mine is wrong. Now it's clear and also just figured out as you mentioned that I just need to multiply inner by 1/s to draw the Nyquist plot.

I just started studying this subject and many things seem unfamiliar to me.

Anyway, I'm so pleasant as hell now and thank you so much again, LvW.!!