Calculations of lossless coupled lines from a physical structure

[Eres_89]

Hi All,



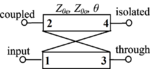
I've a smaill problem with analysis/interpetation of a simple, measured microstrip coupled-lines structure. I just want to be make sure, that I'm trying to solve this problem in proper way. So... I've measured such a structure, and now I want to calculate situation, where losses are not included (well, this will be much more ideal case of coupled-lines). My first thought was to calculate something like coupling loss according to simple equation:

\( CL = 1 - (S_{21})^2 \) where \(S_{21}\) is scaterring parameter defining coupling.

I use calculated values as factor for calculations of ideal response, I mean, I'm taking coupling and divide it with calculated CL. Unfortunatelly, total nonsense comes out - I mean, that obtained response is not resemble any coupling characteristic. So I've tried to change approach and calculated Insertion losses by using:

\(IL = (S_{21})^2 + (S_{31})^2 + (S_{41})^2\)

and once again, i use it to divide \(S_{21}\). I've received results which have much more sense, however I think, that coupling is litlle to large (as if small transmission loss have been included). So, what equations or method should I use to calculate response of ideal coupled-lines from measurements of physical structure ?


Regards,

E.

 

[albbg]

Could you please post a sketch of the structure you are analyzing with the ports location ?

 

[Eres_89]

Yes, please see it below:


On this moment, I use other approach which gives quite good results. However, I'm not sure whether this is good idea. I'm calculating entire losses of the coupled lines coupler by using equation:

\[ Total Loss = \frac{1}{(S_{21})^2 + (S_{31})^2 + (S_{41})^2 +(S_{11})^2}\]

And after that, I'm multiplying derived value with measured \(S_{21}\) and \(S_{31}\) to receive responses of lossless structure i.e."

\[ S_{21(Ideal)} = S_{21(Meas)} \cdot Total Loss \]
\[ S_{31(Ideal)} = S_{31(Meas)} \cdot Total Loss \]

This is good idea ?

--- Updated Nov 16, 2020 ---

Moreover, this is theorethically 3-dB directional coupler (with equal power split). I've observed, that coupling and transmission of fabricated coupler have value of 3.4 dB (not expected 3 dB), so I asked a question to myself "what coupling will have different coupler which is ideal/lossless if measured one will have 6.4 dB ?"

 

[albbg]

I don't understand your equations. How do you derive them ?

When you measure, f.i. by means of a network analyzer, the insertion loss S31 when port 2 and 4 are terminated on 50 ohm load, you are measuring the sum of all the losses of the coupler.
Real components have greater losses than theoretical due to imperfections in the microstrips, losses in the material, etc.

 

[Eres_89]

albbg thank you for response. Well, I know that real components have greater losses than ideal. I just want to calculate how a \( S_{21}\) graph be look like for such an ideal case, when you measure fabricated coupled-lines.
The equations which I've presented in previous posts are taken from my old lecture notes.