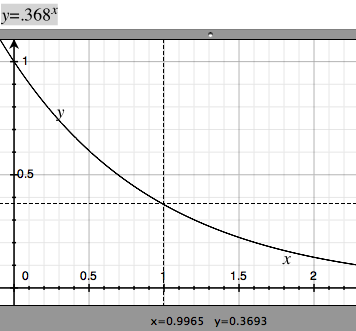
calculating current in RL circuit using numerical methods
- Thread starter SHANKARS
- Start date
Similar threads
-
different methods for stability analysis
- Started by senmeis
- Replies: 4
-
Calculating the drop in accuracy of a 3 wire PT100 RTD
- Started by rf-electo
- Replies: 3
-
Purpose of diodes in supervisor IC circuit
- Started by pacman22
- Replies: 3
-
Using 1N4001 Diode over 1N457 diode in a battery charging circuit
- Started by khatus
- Replies: 5