Audio I/Q phasing networks, which is better?

[neazoi]

Hi I have found two types of BIDIRECTIONAL audio I/Q (45 degrees difference) phase shift networks, which I have enclosed in red squares.

I wonder, which of the two is better, in the sense that keeps the phase difference more constant throughout the 300Hz-3KHz audio region?

A third method is the polyhase network

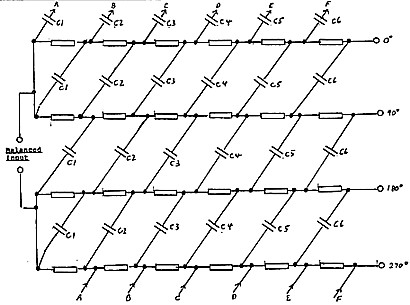
[diagram from: users. tpg. com. au/ldbutler/Fig1SSBMod.jpg]

but does this complex circuit has asignificant advantage over the other simple ones?

Also what other options would you suggest?

- - - Updated - - -

Another option is figure 3 on this page

https://www.analog.com/en/design-ce...cuits-from-the-lab/cn0245.html#rd-description

 

[Terminator3]

I wonder, which of the two is better, in the sense that keeps the phase difference more constant throughout the 300Hz-3KHz audio region?

Maybe computer (dsp) realtime program for microcontroller?
If you still want to use analog schematic, i imagine it can be modelled in some LTSpice, or maybe QUCS. Then performance can be compared

 

[neazoi]

Maybe computer (dsp) realtime program for microcontroller?
If you still want to use analog schematic, i imagine it can be modelled in some LTSpice, or maybe QUCS. Then performance can be compared

One of the circuits is balanced and the other is not.
I wonder what is the benefit for the more complex transformer balanced one?
Does it have to do with the audio phasing or level at both branches, that maybe kept more constant throughout the audio passband?

 

[FvM]

Transformer balancing has nothing to do with phase shift network performance.

Achieving 90 degree phase difference with constant magnitude over a larger frequency interval is a matter of approximation. More circuit elements give smaller phase error and/or larger frequency range. Very good results (e.g. 3 decades with < 1 degree phase error) can be achieved with staggered active all-pass filters.

 

[neazoi]

Transformer balancing has nothing to do with phase shift network performance.

Achieving 90 degree phase difference with constant magnitude over a larger frequency interval is a matter of approximation. More circuit elements give smaller phase error and/or larger frequency range. Very good results (e.g. 3 decades with < 1 degree phase error) can be achieved with staggered active all-pass filters.

I agree with the active filters. However the simplicity of this passive circuit and the fact that it is bidirectional, are both very interesing properties.
So I guess the polyphase network has better phase accuracy because it has more components, like you said.
However, I am thinking that it might be practically better to match a few components, than the many components required by the polyphase, so in practical terms it might be better to use simpler circuits?

 

[betwixt]

The transformers are simply there to split the signal into two phases, lets call them 0 and 180 degrees. The RC networks produce quadrature output from those two phases. In a simple RC network, the phase shifts are 90 degrees at one frequency and at each side of it the shift starts to vary. In the polyphase network the 90 degrees is accurate at several frequencies in the passband so the variation is smaller and better distributed.

You might be interested in a program called "Quadnet" which models and analyzes various quadrature shift networks (although not polyphase directly), it is free from www.TonneSoftware.com

Brian.

 

[zorro]

For SSB modulation by phasing method, not only phase quadrature is important in the audio phasing networks, but amplitude balance vs frequency too in order to suppress the unwanted sideband. Amplitude response could not be flat, but it should be ideally the same at the two outputs.
For example, simple one-pole lowpass and highpass filters with the same time constant have 90 deg phase difference at all frequencies, but magnitude is the same at only one frequency.

 

[FvM]

For example, simple one-pole lowpass and highpass filters with the same time constant have 90 deg phase difference at all frequencies, but magnitude is the same at only one frequency.

Yes, thus all-pass filters with it's natural gain of unity are better suited.