dashxdr
Newbie level 6

Arturia is a company that sells software synthesizers, one of them emulates the Moog. They brag about their approach, calling it True Analog Emulation. One feature they describe is the approach does not generate any aliased frequences, unlike a competitor's product.
The aliased frequencies they speak of are artifacts of the algorithm used to generated the audio samples. If their sampling rate is 48000/second, a naive approach to generating your samples will inadvertantly create higher order frequencies than 24000 hz. These cannot be reproduced at a sampling rate of 48khz, so they'll cause aliased "noise" frequencies that are unwanted.
What I'm trying to figure out is how such an algorithm might work. Meaning how to generate smooth, clean synthesized audio without using massive CPU cycles and without having alias noise.
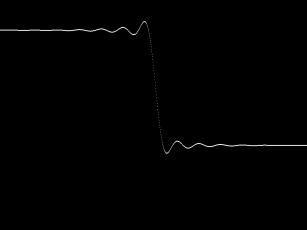
Here is a concrete example. Suppose you generate a square wave like this:
float a = 0;
freq = .1;
for(;
{
output_sample = (a - floor(a)) < 0.5 ? -1 : 1;
a = a + freq;
freq = freq * .9999;
}
It will start high and go lower and lower. If you actually do this and output the samples to a DAC + speaker, it sounds awful. There are screetching frequencies in the background behind the main dropping tone, hissing, some rising, some falling. Just total chaos that is a big distraction.
I believe these artifacts are what Arturia's promotional literature is talking about.
I can get a good result by building up a square wave from sine waves of higher and higher frequency (and lower amplitude) if I cut off at the right point (sort of a low-pass filter). But this is computationally expensive as well as very specific to the waveform in question (not very general).
The general question is how do you approximate a signal that could be defined by patial differential equations, in a continuous sense, using computers that are not continuous in any sense, without introducing distortion?
I don't even know how to properly phrase the question, actually. No formal education in this area.
You've got a circuit composed of resistors, transistors, operational amplifiers, capacitors and coils. You want to model that circuit and produce samples of the signals at say 48khz without introducing artifacts. That is, your sequence of samples would be as nearly identical as possible to a digitized sample stream coming from actual hardware...
Sorry this question took too long to ask. Any advice at all would be welcome. Even any suggestions as to the correct terminology I should be using. Is this in the realm of Finite Impulse Response? Numerical Analysis? Digital Signal Processing? Digital filtering?
Thanks.
The aliased frequencies they speak of are artifacts of the algorithm used to generated the audio samples. If their sampling rate is 48000/second, a naive approach to generating your samples will inadvertantly create higher order frequencies than 24000 hz. These cannot be reproduced at a sampling rate of 48khz, so they'll cause aliased "noise" frequencies that are unwanted.
What I'm trying to figure out is how such an algorithm might work. Meaning how to generate smooth, clean synthesized audio without using massive CPU cycles and without having alias noise.
Here is a concrete example. Suppose you generate a square wave like this:
float a = 0;
freq = .1;
for(;
{
output_sample = (a - floor(a)) < 0.5 ? -1 : 1;
a = a + freq;
freq = freq * .9999;
}
It will start high and go lower and lower. If you actually do this and output the samples to a DAC + speaker, it sounds awful. There are screetching frequencies in the background behind the main dropping tone, hissing, some rising, some falling. Just total chaos that is a big distraction.
I believe these artifacts are what Arturia's promotional literature is talking about.
I can get a good result by building up a square wave from sine waves of higher and higher frequency (and lower amplitude) if I cut off at the right point (sort of a low-pass filter). But this is computationally expensive as well as very specific to the waveform in question (not very general).
The general question is how do you approximate a signal that could be defined by patial differential equations, in a continuous sense, using computers that are not continuous in any sense, without introducing distortion?
I don't even know how to properly phrase the question, actually. No formal education in this area.
You've got a circuit composed of resistors, transistors, operational amplifiers, capacitors and coils. You want to model that circuit and produce samples of the signals at say 48khz without introducing artifacts. That is, your sequence of samples would be as nearly identical as possible to a digitized sample stream coming from actual hardware...
Sorry this question took too long to ask. Any advice at all would be welcome. Even any suggestions as to the correct terminology I should be using. Is this in the realm of Finite Impulse Response? Numerical Analysis? Digital Signal Processing? Digital filtering?
Thanks.
Last edited: